Domanda:
Cosa fa sì che gli insetti proiettino grandi ombre da dove si trovano i loro piedi?
OmnipresentAbsence
2013-03-04 21:44:33 UTC
view on stackexchange narkive permalink

Di recente mi sono imbattuto in questa interessante immagine di una vespa, che galleggia sull'acqua:

enter image description here

Supponendo che non sia photoshoppato, ho un paio di domande:

  1. Perché vedi la sua immagine in questo modo (qual è la spiegazione fisica; sono sicuro che ce ne sia una interessante)? ​​

  2. Perché le macchie che circondano le zampe della vespa sono a forma di cerchio? Sarebbero di forma quadrata se i "piedi" della vespa fossero di forma quadrata?

Non sapevo esattamente quali tag sarebbero stati adatti qui, volevo assegnargli il tag "fenomenons", ma quello è stato rimosso di recente, quindi sentiti libero di modificare i tag.
Sicuramente non è photoshoppato. O se lo è, è possibile scattare foto reali come se fosse. Lo si vede spesso in estate in una forte luce solare quando si è seduti vicino a acque poco profonde e limpide ai bordi di torrenti con fiumi molto puliti e sul loro fondo. Ma, comunque, un'immagine meravigliosamente bella.
Tre risposte:
delete000
2013-03-04 22:02:29 UTC
view on stackexchange narkive permalink

  1. Il meccanismo in gioco qui è la tensione superficiale. La coesione delle molecole d'acqua è ciò che mantiene a galla la vespa. A causa di questa coesione, la superficie dell'acqua si comporta come una membrana ed è curva verso l'interno. I raggi di luce che verrebbero rifratti dalla superficie perfettamente piana sono ora incidenti con un angolo alterato e vengono riflessi o rifratti da angoli alterati attorno alla punta delle zampe della vespa, da cui l'ombra.

  2. La curvatura della superficie traccia la forma dell'oggetto che tocca la superficie. Come puoi vedere, però, l'area dell'ombra è molto più grande delle punte delle zampe della vespa. La forma dell'ombra sarà quindi sempre arrotondata. I raggi di curvatura possono anche essere calcolati, data la differenza di pressione tra aria e acqua.

+1 Penserei anche che i margini luminosi attorno alle ombre dei "piedi" sarebbero dovuti all'acqua curva che focalizza la luce.
Vedi anche, [Caustics] (http://en.wikipedia.org/wiki/Caustic_ (optics)).
DarkLightA
2013-03-04 21:52:57 UTC
view on stackexchange narkive permalink

Questa è un'immagine davvero sorprendente! Non sono affatto un esperto, ma ho un'idea.

Quando la vespa si trova sull'acqua, è leggermente curva verso il basso. La luce che colpisce queste parti sarà quindi piegata più verso l'esterno che se colpisse solo l'acqua normale. Questo accade su ogni lato del cerchio, quindi la luce è sempre piegata verso l'esterno e non raggiunge il fondo in quei punti.

Pertanto, ottieni questo effetto.

Inoltre , per rispondere alla tua seconda domanda, i piedi sono così piccoli rispetto all'ombra che non giocano un ruolo importante nella forma.

leftaroundabout
2013-03-05 08:14:51 UTC
view on stackexchange narkive permalink

Questo è un ottimo esempio di quanto possa essere bello ragionare su argomenti di rifrazione usando il principio di Fermat.

Riduciamo tutto questo a 2 dimensioni. La tensione superficiale produce qualcosa del genere: 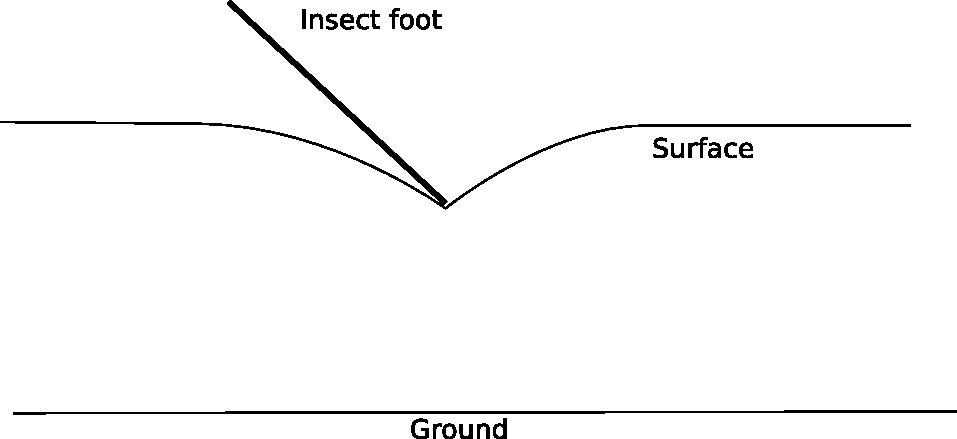2Dschem-plain

Ora, se vogliamo sapere dove deve andare un "raggio" di luce per arrivare da una fonte di luce, dobbiamo solo trovare il modo in cui lo prende il tempo minimo. La luce è più lenta nell'acqua, quindi vuole andare il più lontano possibile nell'aria - ovviamente, solo se non è troppo lungo. Così lontano dall'insetto, un raggio di luce sarebbe semplicemente entrato nell'acqua perpendicolarmente, poiché ciò riduce al minimo sia la lunghezza totale del percorso che il percorso in acqua. 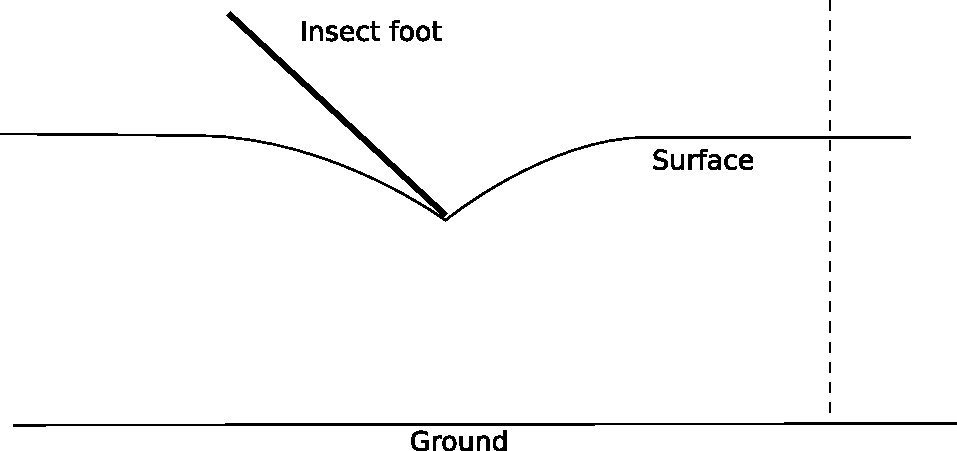2Dschem-straightray

Tuttavia, proprio sotto il piede dell'insetto, ciò ha vinto non funziona - il piede stesso non è traslucido † - e, cosa più importante, un po 'a sinistra oa destra da destra sotto il piede il percorso più veloce sarà ancora proprio attraverso il piede, poiché qualsiasi altro percorso richiederà alla luce di viaggiare sostanzialmente di più attraverso l'acqua, mentre la lunghezza totale del percorso è solo leggermente più breve. 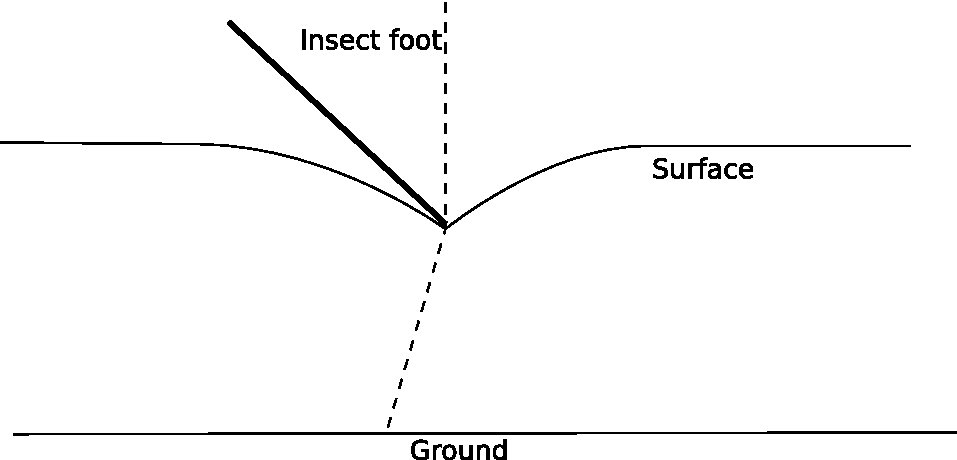2Dscheme-forbiddencurveray

quindi tutti questi raggi sono "invisibili". Che funzioni in questo modo dipende da quanto siamo lontani da destra sotto il piede, in modo che si crei un'ombra circolare, anche quando il piede stesso ha un'altra forma.

† In realtà, è un po 'traslucido suppongo, ma sappiamo che il piedino sarà colpito solo da una piccola quantità di luce. Quindi, se quel po 'di luce deve essere diffuso su un intero terreno, non ci sarà molta intensità laggiù.
IMO, quello che succede nel punto in cui il piede dell'insetto tocca l'acqua non è molto interessante né illuminante. Perché dovrebbe piegarsi a sinistra e non a destra? Sarebbe più chiaro disegnare cosa succede alla luce rifratta man mano che si avvicina sempre più al piede. A causa della curva sull'acqua, la luce viene rifratta sempre più lontano dalla linea retta, non è il piede che proietta l'ombra, è l'acqua che rifrange la luce dal punto in cui i piedi toccano l'acqua. Che il piede sia traslucido o meno è irrilevante. Un effetto simile chiamato caustico si verifica senza alcun piede.
Non sono d'accordo: "man mano che si avvicina al piede" porterebbe a qualche scherzo con la legge di Snell, che è fisicamente molto meno illuminante del principio di Fermat. - Giusto - come ho detto, il piede in sé non ha importanza. Ciò che conta è che ci sia un "luccio" in cui un intero gruppo di raggi luminosi hanno il loro percorso più veloce (e quindi nessuno di loro riceve molta energia). Per quanto riguarda il "perché dovrebbe piegarsi a sinistra", penso sia chiaro che questo è solo un esempio di raggio, come quello dritto.
Sì, ma il luccio stesso gioca solo una piccola parte nell'intero processo poiché la maggior parte della rifrazione viene eseguita dal resto delle curve.
La rifrazione è semplicemente un modo speciale per osservare la propagazione dei fotoni che _ funziona_ solo per superfici lisce (differenziabili). Per descrivere qualcosa di simile a questo fenomeno devi prima fare qualche brutta discussione sui limiti (ovviamente, la maggior parte dei fisici non farebbe questo passo esplicitamente). D'altra parte, il principio di Fermat funziona direttamente (poiché corrisponde alla più fondamentale propagazione del percorso di Feynman dei fotoni) e può quindi essere utilizzato per descrivere immediatamente l'ombra circolare.
Ma anche se levighi leggermente il luccio, l'ombra sarebbe comunque molto visibile. Il luccio non è necessario né la causa principale della grande ombra. Questa risposta, sebbene buona, IMO si concentra troppo sulla discontinuità, che credo contribuisca molto poco all'ombra rispetto al resto della curva.
Con un luccio levigato non sarebbe più un'ombra, però, solo un'area meno illuminata, forse sfocata. Solo per il limite di $ r _ {\ mathrm {pike}} \ ll r _ {\ mathrm {dip}} $ si ottengono le ombre circolari effettive di cui tratta questa domanda.


ⓘ
Questa domanda e risposta è stata tradotta automaticamente dalla lingua inglese. Il contenuto originale è disponibile su stackexchange, che ringraziamo per la licenza cc by-sa 3.0 con cui è distribuito.
Loading...