Fornirò una possibile risposta controversa, nel tentativo di provocare qualche discussione. Lo faccio in buona fede e nella convinzione che ciò che dichiaro sia vero e ritorno con riferimenti (i commenti di "citazione necessaria" saranno molto utili). Contesto questo con: Sono un teorico della materia condensata e penso che la solita esposizione di AdS / CFT abbia il carrello davanti ai buoi. Farò una lunga deviazione, ma spero di tornare alla fine e rispondere alla domanda vera e propria.

Iniziamo con una catena di spin 1/2 su un reticolo 1D, di estensione infinita. Lo spazio di Hilbert è un prodotto di spazi bidimensionali. Lascia che l'Hamiltoniano sia Ising anti-ferromagnetico con un campo magnetico esterno, in modo che a un'intensità di campo critica avremo una transizione di fase quantistica da anti-ferromagnetico a ferromagnetico. Ci occupiamo solo dello stato fondamentale (cioè a temperatura zero). Facciamo quindi un paio di osservazioni: lontano dalla transizione di fase, la lunghezza di correlazione è finita e l'entropia di entanglement di ogni dato blocco di lunghezza $ L $ è asintoticamente una costante (come $ L \ rightarrow \ infty $); alla transizione di fase, la lunghezza di correlazione è infinita e l'entropia di entanglement diventa $ \ log (L) $. Si noti che queste sono caratteristiche piuttosto speciali dello stato fondamentale, poiché lo stato tipico (definito come medio sulla misura canonica di Haar) ha un'entropia di entanglement che scala come $ L $.

Pertanto, invece di scrivere lo stato fondamentale con la massima generalità $$ \ left | \ Omega \ right \ rangle = \ sum_ {s_1, s_2, \ ldots} c_ {s_1, s_2, \ ldots} \ left | s_1 \ right \ rangle \ otimes \ left | s_2 \ right \ rangle \ otimes \ ldots $$ dove dovremmo specificare la matrice $ c $ con un numero di dimensioni esponenzialmente grande (che copre l'intero spazio di Hilbert), limiteremo la nostra attenzione ai cosiddetti Matrix Product States (MPS) con la forma: $$ \ left | \ Omega \ right \ rangle = \ sum_ {s_1, s_2, \ ldots} \ mathrm {Tr} \ left (\ hat A ^ {s_1} \ hat A ^ {s_2} \ ldots \ right) \ left | s_1 \ right \ rangle \ otimes \ left | s_2 \ right \ rangle \ otimes \ ldots $$ dove le matrici $ \ hat A ^ {s_i} $ sono matrici arbitrarie di dimensione $ m $. Essenzialmente, stiamo fissando l'angolo dello spazio di Hilbert che è attraversato da un numero di dimensioni linearmente crescente. Ora, come $ m \ rightarrow \ infty $ recuperiamo l'intero spazio di Hilbert, ma lontano dal punto critico, un $ m $ finito è sufficiente per descrivere completamente (esattamente) lo stato fondamentale, a causa del punto precedente sull'entropia di entanglement finito; essenzialmente, la dimensione $ m $ controlla quanto entanglement è possibile tra siti adiacenti, e l'MPS ansatz abbraccia completamente tutti questi stati.

Ma, come detto, l'entanglement in uno stato critico non è limitato. In questo caso, possiamo utilizzare una risposta diversa, la Multi-scale Entanglement Renormalisation Ansatz (MERA). La costruzione è difficile da descrivere a parole, ma più semplice nelle immagini. Se usiamo diagrammi di rete tensoriale (identificati per la prima volta da Penrose e chiamati reti di spin), rappresentiamo ogni tensore come un blob con un numero di gambe uguale al suo rango. Trattando le matrici $ \ hat A ^ {s_i} $ come tensori a 3 ranghi (uno in più a causa dell'indice di spin), possiamo disegnare l'MPS come:

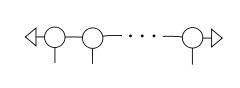
dove le gambe inferiori sono gli indici di rotazione. Il MERA è quindi

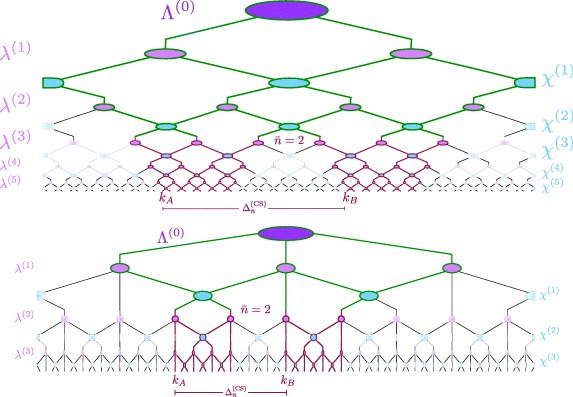
(ma immagina che "l'albero" continui verso l'alto senza fine). L'essenza è che reifichiamo la grana grossa (cioè la rinormalizzazione) nella descrizione dello stato fondamentale mediante un albero di districatori e grana grossa. Ancora una volta, se lo facciamo bene, questo può descrivere lo stato fondamentale con perfetta accuratezza.

Questi diagrammi di rete tensoriale danno anche una ragione pittoresca per cui l'entropia di entanglement scala come costante e come $ \ log (L ) $ rispettivamente. L'argomento è che l'entanglement è localizzato al confine di un blocco (come deve, poiché ogni connessione in quella rete può supportare solo una quantità finita di entanglement), ma il "confine" in realtà scala in modo diverso nei due casi: il caso non critico, sono solo i bordi di una catena 1D, che chiaramente non si preoccupano della massa; nel caso critico, deve includere non solo il livello inferiore, ma tutti i livelli sopra di esso, e ci sono $ \ log (L) $ livelli.

Finora, tutto è fondamentalmente (fino ai casi d'angolo) vero. Passiamo ora a cose più congetturali / interpretative. Concentrati su MERA. Si noti che se lo trattiamo come uno spazio, una misura di distanza naturale è il numero di "salti" che dobbiamo fare da un vertice all'altro; si noti inoltre che nel limite del continuo questo è uno spazio iperbolico omogeneo, cioè AdS. Nel modello di Ising originale, nel punto critico, la teoria dei campi dovrebbe essere conformalmente invariante e quindi essere una CFT. Questo è tutto tranne AdS / CFT, tranne per il fatto che non abbiamo specificato che i coefficienti MERA sono calcolati da una teoria gravitazionale quantistica (probabilmente non può essere, penso ... la carica centrale è 1 e nulla è supersimmetrico).

Ora, a questo punto, potresti pensare "Ah! Vedi? AdS / CFT è di primaria importanza anche per cose banali come la materia condensata!" Tuttavia, vorrei presentare alcune prove che in realtà AdS / CFT è una conseguenza banale di un'idea molto intelligente, che è interpretare geometricamente le informazioni in uno stato fondamentale.

Consideriamo invece un sistema fermionico interagente in 1D. I soliti elettroni con repulsione di Coulomb andranno bene. È noto che lo stato fondamentale fisico è quello dei solitoni non interagenti di elettroni frazionati: oloni (che trasportano la carica) e spinoni (che trasportano lo spin). La nostra ansatz sarà quindi quella di MERA, ma a una certa profondità dell'albero, duplichiamo tutto ciò che è al di sopra di esso --- in modo da ottenere due sistemi 1D, uno per gli oloni e uno per gli spinoni. Nell'immagine geometrica sopra, sarà come se avessimo incollato uno spazio aggiuntivo per AdS sul solito, in modo da ottenere una forchetta.

Il motivo per cui questo suggerisce che in realtà lo stato fondamentale dovrebbe venire prima e il principio dell'olografia secondo è duplice:

1. L'olografia vale solo per stati speciali come lo stato fondamentale, dove l'entanglement entropy scale sub-bulk.
2. Lo spazio AdS interno potrebbe non essere AdS, o anche ammettere alcun tipo di bella immagine geometrica, e anche se lo fa, potrebbe non essere dato da una sorta di Lagrangiano teoria dei campi basata.

Quindi, tornando alla domanda: "cosa c'è di speciale in AdS?" Altre risposte si concentreranno senza dubbio sulla geometria speciale che fa funzionare la matematica, ma risponderei che la chiave non è mai lo spazio interno, ma il confine: il (super-) CFT. Lo spazio interno, in questo caso, AdS, arriva solo per un giro. Se avessimo un altro tipo di teoria dei confini, avremmo un altro tipo di spazio interno, o non uno spazio del tutto!

Riferimenti:

Articolo seminale (?) Su corrispondenza tra MERA e olografia: http://arxiv.org/abs/0905.1317 Ramificazione di MERA come olografia esotica: http://pirsa.org/10110076

AdS $ _d $ in qualsiasi dimensione spazio-temporale $ d \ geq 2 $ è simmetrico al massimo con il gruppo isometrico quindi (d-1,2) (per la firma di Minkowski).

Questo gruppo coincide con il gruppo conforme nelle dimensioni d-1 (sempre per la firma di Minkowski).

Per esempio, per AdS $ _5 $ si ottiene il gruppo isometrico so (4,2), che è il gruppo conforme in 4 dimensioni . Questa corrispondenza è un controllo di coerenza un po 'banale che qualcosa come una corrispondenza $ _5 $ / CFT $ _4 $ di AdS può funzionare.

Un'altra caratteristica speciale di AdS rispetto a dS è che fornisce un vuoto stabile nella maggior parte teorie (mentre dS è solo meta-stabile) e che è compatibile con SUSY (mentre dS non lo è).

Anche gli spazi che asintoti ad AdS hanno proprietà molto speciali. Brown e Henneaux hanno mostrato in d = 3 che qualsiasi teoria quantistica coerente della gravità deve essere duale per una teoria del campo conforme bidimensionale, nel senso che lo spazio di Hilbert deve cadere in rappresentazioni irriducibili di due copie dell'algebra di Virasoro, con carica centrale determinato dalla costante di Newton e dalla costante cosmologica. Questo è stato un importante precursore della corrispondenza AdS / CFT, in cui tale dualità è realizzata esplicitamente (ma in dimensioni superiori).

Lo spazio di Minkowski è anche simmetrico e stabile al massimo, ma non così suscettibile all'olografia come AdS .

In sintesi, gli spazi AdS sono semplici e hanno proprietà fisiche interessanti, motivo per cui vengono utilizzati abbastanza frequentemente.

Esistono alcune estensioni della corrispondenza AdS / CFT, quindi è più accurato chiamare l'insieme più generale di dualità corrispondenza indicatore / gravità. In tutte queste dualità si ha un duale gravitazionale di qualche teoria quantistica dei campi, e la teoria in questione determina le condizioni al contorno su tutti i campi di massa (inclusi gli asintotici della geometria di massa). Gli stati di quelle teorie corrispondono a piccole fluttuazioni (modi normalizzabili) che si muovono nella maggior parte di quello spaziotempo, e lo stato del vuoto di solito corrisponde allo spazio massimamente simmetrico ("vuoto"). Ci sono molti di questi esempi che non sono AdS nemmeno asintoticamente, sebbene purtroppo asintoticamente dS non sia ancora uno di questi (in parte perché non è chiaro cosa significhi realmente l'espressione "asintoticamente dS"). Esistono esempi asintoticamente piatti, purtroppo con sfondo dilatativo lineare.

Ma, all'interno dell'insieme di tutte le dualità olografiche c'è qualcosa di speciale negli spazi che sono asintoticamente AdS. Quelle corrispondono a teorie che diventano conformi a brevi distanze. Usando il linguaggio wilsoniano, quelle sono teorie il cui flusso di gruppo di rinormalizzazione può essere continuato a tutte le scale energetiche, quindi sono teorie di campo quantistiche completamente ben definite senza interruzioni. Tali teorie dei campi sono definite come deformazioni rilevanti dei punti fissi nell'UV e la traduzione olografica di tale affermazione è che il duale gravitazionale è asintoticamente AdS.

Continuando con il linguaggio wilsoniano, di solito è necessario utilizzare la QFT solo come un'efficace teoria dei campi, che viene quindi intrinsecamente definita con un cutoff UV. Tale teoria quantistica dei campi più generale (definita solo fino a una certa scala di energia) corrisponde a istanze di dualità gauge-gravità che non sono asintoticamente AdS. La corrispondenza tra EFT con uno spazio di interruzione e non asintoticamente AdS (almeno in alcune occasioni soprannominata "corrispondenza non AdS / non CFT") è meno ben compresa di AdS / CFT (con la quantità di lavoro su AdS / CFT, questo vale per molti altri soggetti ...). Ma è un argomento molto utile e interessante, per certi versi più della corrispondenza originale AdS / CFT, quella che ha aperto i cancelli.

In ogni caso, il tipo di condizioni al contorno imposte lo spazio è restrittivo solo quando si discutono questioni globali. Qualsiasi processo locale a cui sei interessato (ad esempio, la formazione e l'evaporazione dei buchi neri) può essere incorporato nello spazio AdS asintoticamente con una costante cosmologica arbitrariamente piccola. Non penserei quindi alla serie di esempi forniti da AdS / CFT come "non fisica" in alcun modo - potrebbe non rispondere a tutte le possibili domande a cui uno potrebbe essere interessato, ma è il modo migliore per affrontare tutta una serie di affascinanti quelli.

Lo spazio pubblicitario è fondamentalmente solo uno spazio iperbolico, con una direzione temporale. Ecco un bel fatto geometrico. Considera lo spazio iperbolico 2d nel modello del disco di Poincaré. (Generalizzare a dimensioni superiori è semplice.) La metrica è $ ds ^ 2 = \ frac {dr ^ 2 + r ^ 2 d \ theta ^ 2} {(1-r ^ 2) ^ 2} $. L'elemento dell'area corrispondente è $ \ frac {rdrd \ theta} {(1-r ^ 2) ^ 2} $. Quindi considera il cerchio a $ r = r_0 $ fisso. Ha circonferenza $ 2 \ pi r_0 \ frac {1} {1-r_0 ^ 2} $ e area $ 2 \ pi \ int_0 ^ {r_0} \ frac {rdr} {(1-r ^ 2) ^ 2} $. Per $ r_0 = 1 - \ epsilon $, con $ \ epsilon \ ll 1 $, questi sono $ \ frac {\ pi} {\ epsilon} - \ frac {\ pi} {2} + {\ cal O} (\ epsilon) $ e $ \ frac {\ pi} {2 \ epsilon} - \ frac {\ pi} {2} + {\ cal O} (\ epsilon) $, rispettivamente.

A cosa serve significare? Significa che, per cerchi grandi rispetto al raggio di curvatura dello spazio, il perimetro e l'area si ridimensionano nello stesso modo in cui si ingrandisce il cerchio. (Al contrario dello spazio piatto, dove uno scala come il quadrato dell'altro.) Penso che questo sia un accenno all'olografia; in un certo senso, AdS è lo spazio in cui l'olografia diventa quasi banale, perché i volumi dimensionali $ d $ e $ d-1 $ sono quasi identici, motivo per cui comprendiamo l'olografia molto meglio in AdS.

( Ovviamente questo non è estraneo alle idee sulla simmetria conforme, ecc. Ma penso che questo fatto geometrico faccia luce ed è facile da capire senza entrare nei dettagli della fisica.)

$ AdS $ in una forma euclidea è uno spazio iperbolico. In due dimensioni il piano iperbolico $ {\ cal H} ^ 2 $ è una varietà semplicemente connessa con curvatura gaussiana costante $ -1 $. Il $ AdS_2 $ bidimensionale si trova vicino all'orizzonte degli eventi di un buco nero, che è il disco di Poincaré $ {\ cal D} ^ 2 ~ = ~ \ {z: | z | ~ < ~ z_0 \} $, e relativo a lo spaziotempo di Rindler il semipiano superiore $ {\ cal H} ^ 2 ~ = ~ \ {z: Im (z) ~ > ~ 0 \} $. Il gruppo di isometrie $ Iso ({\ cal H} ^ 2) $ è l'insieme delle trasformazioni uniformi $ z ^ \ prime ~ = ~ gz $ che soddisfano la metrica iperboloide per $ s ~ = ~ s (z, ~ gz) $. Il semipiano e il disco di Poincar {\ 'e} sono collegati da una trasformazione conforme, quindi la trasformazione delle coordinate è data dallo stesso gruppo. Nel semipiano le isometrie sono le trasformazioni lineari frazionarie, o gruppo modulare
$$ g: {\ cal H} ~ \ rightarrow ~ {\ cal H}, ~ z: ~ \ mapsto ~ gz: ~ = ~ { {az ~ + ~ b} \ over {cz ~ + ~ d}}, ~ \ left (\ matrix {a &b \ cr c & d} \ right) ~ \ in ~ SL (2, ~ {\ bf R} ). $$ Le matrici $ g $ e $ -g $ sono le stesse trasformazioni lineari frazionarie, quindi le isometrie $ Iso ({\ cal H} ^ 2) $ possono essere identificate con il gruppo di Klein proiettivo $ PSL (2, ~ {\ mathbb R}) ~ = $ $ SL (2, ~ {\ mathbb R}) / \ {\ pm 1 \} $. Il gruppo è ulteriormente limitato dal sottogruppo di isotropia che lascia gli elementi di $ {\ cal H} ^ 2 $ invariati $ z ~ = ~ gz $. Qualsiasi $ g ~ \ in ~ PSL (2, ~ {\ mathbb R}) $ definisce il gruppo di rotazione $ SO (2) $. Quindi $ {\ cal H} ^ 2 ~ = ~ PSL (2, ~ {\ mathbb R}) / SO (2) $.

La struttura discreta, o $ PSL (2, {\ mathbb Z}) $ si manifesta nella simmetria a tassellatura del semipiano o disco iperbolico. Queste simmetrie si vedono nelle stampe di Escher chiamate cerchi limite. Queste strutture discrete danno la struttura MERA a cui Genneth fa riferimento. L '"accumulo" della struttura verso il confine è una rinormalizzazione del sistema di spin di Ising, per gli spin ai vertici nella tassellatura. Quello che segue è in parte una breve descrizione del completamento discreto di $ AdS $ dovuto a Charles Frances.

http://www.math.u-psud.fr/~frances/

Lo spazio limite $ \ AdS parziale_ {n + 1} $ è un Minkowski spaziotempo, o uno spaziotempo $ E_n $ che è semplicemente connesso a $ AdS $ è tale che $ AdS_ {n + 1} \ cup E_n $ è il completamento conforme di $ AdS_ {n + 1} $ sotto l'azione discreta di un gruppo kleiniano. Per il gruppo lorentziano $ SO (2, ~ n) $ esiste il gruppo discreto $ SO (2, n, Z) $ che è un gruppo di Mobius. Per un sottogruppo discreto $ \ Gamma $ subset $ SO (2, ~ n, ~ Z) $ che obbedisce a determinate proprietà regolari per i punti di accumulo nell'insieme discreto $ AdS_ {n + 1} / \ Gamma $ è un'azione conforme di $ \ Gamma $ sulla sfera $ S_n $. Questa è quindi una mappa che costruisce una corrispondenza $ AdS / CFT $. Dato che $ AdS_n ~ = ~ O (n, 2) / O (n, 1) $ questa struttura coset è una forma di Clifford-Klein, o struttura a doppio coset.

Le geodetiche simili alla luce in $ E ^ n ~ = ~ M ^ n $, lo spaziotempo di Minkowski, sono copie di $ RP ^ 1 $, che in un dato punto p definiscono un insieme che è il cono di luce $ C (p) $. Il punto p è l'azione proiettiva di $ \ pi (v) $ per $ v $ un vettore in una patch locale $ R ^ {n, 2} $ e quindi $ C (p) $ è quindi $ \ pi (P \ cap C ^ {n, 2}) $, per $ P $ normale a $ v $, e $ C ^ {n, 2} $ la regione su $ R ^ {n, 2} $ dove l'intervallo svanisce.

Lo spazio delle geodetiche simili alla luce è un insieme di invarianti e quindi dovuto a uno stabilizzatore su $ O (n, 2) $, quindi lo spazio delle curve simili alla luce $ L_n $ è identificato con il quoziente $ O ( n, 2) / P $, dove $ P $ è un sottogruppo definito il quoziente tra un sottogruppo con topologia Zariski o un sottogruppo Borel e il gruppo principale $ G ~ = ~ O (n, ~ 2) $. Questo quoziente $ G / P $ è una varietà algebrica proiettiva, o varietà di flag e $ P $ è un sottogruppo parabolico. L'incorporamento naturale di un gruppo $ H ~ \ rightarrow ~ G $ composto con la varietà proiettiva $ G ~ \ rightarrow ~ G / P $ è un isomorfismo tra $ H $ e $ G / P $. Questo è quindi un prodotto semi-diretto $ G ~ = ~ P ~ \ rtimes ~ H $. Per $ G $ qualsiasi $ GL (n) $ il gruppo parabolico è un sottogruppo di matrici triangolari superiori. Questo è il gruppo di Heisenberg.

Questa connessione ai gruppi di Heisenberg e ai gruppi parabolici è particolarmente interessante. La struttura qui ha una realizzazione della funzione $ \ theta $ ed è correlata alla densità degli stati nella teoria delle stringhe. Questo porta a mio parere in una struttura molto profonda che non è affatto completamente esplorata.