La contrazione di Lorentz e la dilatazione del tempo possono essere dedotte senza la trasformazione di Lorentz. Puoi dedurre anche il teorema dell ' addizione delle velocità
$$ w ~ = ~ \ dfrac {u + v} {1 + uv / c ^ 2} $$
senza trasformazione di Lorentz? Usando solo la costanza della velocità della luce.
Poiché le trasformazioni di Lorentz sono una conseguenza del postulato di costanza della velocità della luce, insieme ad alcuni postulati di omogeneità e paralleli, è un po 'difficile rendere precisa la richiesta di una dimostrazione gratuita della trasformazione di Lorentz.
Ma interpreterò la domanda come una richiesta di una prova sintetica dell'addizione delle velocità. Una dimostrazione sintetica è una dimostrazione nello stesso stile delle prove geometriche euclidee che fai alle elementari. Ti fornisce un'immagine e un modo intuitivo per comprendere la formula.
Innanzitutto, per iniziare, dovresti capire che una velocità è il rapporto tra la distanza percorsa nel tempo trascorso, è l'analogo della tangente di un angolo in geometria. In geometria, esiste una legge di addizione delle tangenti:
$$ \ tan (a + b) = {\ tan (a) + \ tan (b ) \ over 1 - \ tan (a) \ tan (b)} $$
Il modo più semplice per capire la relatività è che è la geometria di Lorentz --- una geometria in cui il teorema di Pitagora ha un segno meno e le linee perpendicolari non sembrano perpendicolari, ma hanno la stessa pendenza rispetto alla linea di 45 gradi (sui lati opposti), dove la linea di 45 gradi distinta è il raggio di luce.
Nella geometria lorentziana, la formula di addizione è la legge di addizione delle tangenti iperboliche:
$$ \ tanh (a + b) = {\ tanh (a) + \ tanh (b) \ over 1 + \ tanh (a) \ tanh (b)} $$
Se interpreti gli angoli come le rapidità ( questa è solo la definizione dell'analogo lorentziano dell'angolo), le tangenti iperboliche come velocità, questa è la legge dell'addizione delle velocità.
Prima rivedi queste due risposte: I postulati di Einstein $ \ leftrightarrow $ Minkowski space for a Layman e: Quali sono i meccanismi con cui si verificano la dilatazione del tempo e la contrazione della lunghezza?. Hai bisogno di un po 'di intuizione per la geometria.
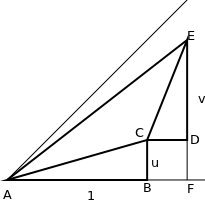
Considera il seguente diagramma:
Il geometrico aggiunta di tangenti
Dove la lunghezza del segmento AB è 1, la lunghezza del segmento BC è u e l'angolo ABC è giusto. Ciò implica che l'angolo CAB ha una tangente di u, per definizione, e che la lunghezza di AC è $ \ sqrt {1 + u ^ 2} $ .
Se voglio che l'angolo CAE abbia tangente v, allora ho bisogno che il rapporto tra EC e CA sia v. Questo determina che la lunghezza di EC sia $ v \ sqrt {1 + u ^ 2} $ , e da questo, impari che la lunghezza di CD è v e la lunghezza di DE è uv (poiché il triangolo ABC e CDE sono simili). Puoi riempire tutte le lunghezze con una penna, il mio programma di disegno non ammette radici quadrate.
Pertanto, la tangente della somma dei due angoli è il rapporto
$$ {EF \ over AF} = {u + v \ over 1 - uv} $$
E spero che il diagramma lo renda evidente senza formule complicate.
Per la relatività, fai la stessa cosa nello spazio-tempo. Il diagramma analogo è fornito di seguito.
L'addizione relativistica delle velocità --- asse del tempo orizzontale
Nel triangolo ABC, AB è lungo il Asse tempo (l'ho disegnato orizzontale per rendere il diagramma il più simile possibile al precedente), e ha lunghezza 1. BC ha lunghezza u, quindi la velocità della linea AC è u.
Da questo, trovi la lunghezza di AC usando la versione relativistica del teorema di Pitagora (con un segno meno). CE viene quindi disegnato relativisticamente perpendicolare ad AC (è così che sembra --- abituatevi a questo), e il triange CED è simile a ABC (per la stessa ragione della geometria euclidea), quindi le lunghezze sono proporzionali. Da questo si impara che DE ha lunghezza v e CD ha lunghezza uv (proprio come prima).
Ora la velocità totale è data dal rapporto tra EF e AF, come prima, ed è ora:
$$ {EF \ over AF} = {u + v \ over 1 + uv} $$
Per convincerti che questo è davvero ok, devi familiarizzare con le rotazioni della relatività.
Approvo la risposta di Ron: è il modo sistematico di procedere. La velocità $ v / c $ può essere scritta come $ \ tanh \ eta $ dove $ \ eta $, la rapidità o qualsiasi altra cosa, è la controparte iperbolica (Minkowski) dell'angolo (euclideo). L'aggiunta di velocità si riduce quindi a una formula di addizione per $ \ tanh (\ eta_1 + \ eta_2) $ perché le rapidità si sommano semplicemente in modo additivo.
Consentitemi di offrire una derivazione elementare senza alcuna rapidità fantasia. Immagina che un oggetto si muova alla velocità $ u $ verso destra, un altro oggetto si sposti di $ v $ verso sinistra rispetto al nostro riquadro. Qual è la loro velocità relativa?
La linea del mondo del primo osservatore è una linea retta contenente i punti $ (0,0) $ e $ (1, u) $; le coordinate sono $ (t, x) $. L'altro oggetto ha una linea universale che collega $ (0,0) $ con $ (1, -v) $. Ora, immaginiamo di trasformare la situazione nel frame di riposo del secondo osservatore, cioè di potenziarlo della velocità $ v $. Come si inclinerà la linea del mondo del primo osservatore?
Per trovare la risposta, notare che facendo il boost di Lorentz che fissa l'origine $ (0,0) $, il prodotto interno lorentziano dei due vettori, $ (1, u) $ e $ (1, -v) $, non cambieranno; Definisco il prodotto interno di $ (A, B) $ e $ (C, D) $ come $ AC-BD / c ^ 2 $ dove il segno meno deriva dai colpi di scena della relatività lorentziana e $ c ^ 2 $ è il convenzionale conversione della lunghezza in tempo. Anche la loro lunghezza non cambierà. Significa anche che il prodotto interno diviso per il prodotto delle lunghezze non cambierà. Nel frame originale, è uguale a $$ \ frac {(1, u) \ cdot (1, -v)} {| (1, u) | \ cdot | (1, -v) |} = \ frac {1 ^ 2 + uv / c ^ 2} {\ sqrt {1-u ^ 2 / c ^ 2} \ sqrt {1-v ^ 2 / c ^ 2}} $$ Nota che prendendo il rapporto, ho annullato la normalizzazione assoluta dei due vettori $ (1, u) $ e $ (1, -v) $, quindi questa normalizzazione non ha importanza. Tuttavia, questo rapporto deve essere lo stesso nel nuovo frame in cui i vettori degli osservatori che indicano le direzioni della linea del mondo sono $ (1,0) $ e $ (1, V) $ dove $ V $ è la velocità relativa totale. Da questi due vettori, lo stesso rapporto di cui sopra (che annulla nuovamente la normalizzazione) è uguale a $$ \ frac {(1,0) \ cdot (1, V)} {| (1,0) | \ cdot | (1, V) |} = \ frac {1} {\ sqrt {1-V ^ 2 / c ^ 2}} $$ Giusto per essere sicuri, i rapporti devono essere uguali e possono anche essere scritti come $ \ cosh \ eta $ dove $ \ eta $ è l '"angolo iperbolico" totale, cioè la rapidità tra le due linee del mondo, lo stesso "angolo" discusso sopra. La formula per $ \ cosh $ è analoga alla formula del liceo per $ \ cos $ che coinvolge il prodotto interno ma non è necessario sapere nulla di questo paragrafo per seguire la mia derivazione.
Ora, noi avere $$ \ frac {1} {\ sqrt {1-V ^ 2 / c ^ 2}} = \ frac {1 ^ 2 + uv / c ^ 2} {\ sqrt {1-u ^ 2 / c ^ 2 } \ sqrt {1-v ^ 2 / c ^ 2}} $$ Quadrato e invertito: $$ 1 - \ frac {V ^ 2} {c ^ 2} = \ frac {(1-u ^ 2 / c ^ 2) (1-v ^ 2 / c ^ 2)} {(1 + uv / c ^ 2) ^ 2} $$ Espandere il prodotto nel numeratore e sottrarre uno da entrambi i lati: $$ - \ frac { V ^ 2} {c ^ 2} = \ frac {1 - u ^ 2 / c ^ 2 - v ^ 2 / c ^ 2 + u ^ 2 v ^ 2 / c ^ 4 - 1 - 2uv / c ^ 2- u ^ 2 v ^ 2 / c ^ 4} {(1 + uv / c ^ 2) ^ 2} $$ Il numeratore del lato destro semplifica, due coppie di termini annullano: $$ - \ frac {V ^ 2 } {c ^ 2} = \ frac {- u ^ 2 / c ^ 2 - v ^ 2 / c ^ 2 - 2uv / c ^ 2} {(1 + uv / c ^ 2) ^ 2} $$ Ora, moltiplicare entrambi i lati per $ (- 1) $ per eliminare i segni. E anche io ora sono in grado di calcolare la radice quadrata: $$ \ frac {V} {c} = \ frac {u / c + v / c} {1 + uv / c ^ 2} $$ che volevamo dimostrare . Sentiti libero di moltiplicarlo di nuovo per $ c $.
David Mermin ha escogitato un bellissimo esperimento mentale, che può essere trovato nel suo libro Boojums fino in fondo :
Supponi che un osservatore in una cornice inerziale $ S $ guarda un treno muoversi a velocità costante $ v $. La lunghezza del treno in movimento, misurata in $ S $, è uguale a $ L $. Ora, al tempo $ t = 0 $, un fotone e una particella massiccia (con velocità $ w < c $) iniziano a muoversi dalla parte posteriore del treno verso la parte anteriore.
Il fotone raggiunge la parte anteriore alla volta $ t = T $, e viene poi riflesso indietro; nel frattempo, la particella massiccia si sta ancora muovendo verso la parte anteriore. In un momento successivo $ t = T + T '$, la particella e il fotone riflesso si incontreranno in un punto specifico del treno. Esprimiamo questa posizione come una frazione $ f $ della lunghezza totale $ L $. Poiché questa posizione è la stessa in ogni sistema di riferimento, possiamo affermare che $ f $ è invariante (se assumiamo ragionevolmente che i rapporti tra le lunghezze non cambino da un sistema di riferimento all'altro).
Da questo, abbiamo $$ w (T + T ') = c (T - T') \ tag {1}. $$ In effetti, sia la particella che il fotone hanno percorso la stessa distanza netta durante il tempo totale $ T + T '$, ma il fotone si stava muovendo nella direzione opposta durante l'intervallo di tempo $ T' $. La distanza percorsa dal fotone durante $ T $ dalla parte posteriore alla parte anteriore è la lunghezza $ L $ del treno + la distanza percorsa dal treno durante questo periodo: $$ cT = L + vT \ tag {2}. $ $ Allo stesso modo, la distanza che il fotone si è mosso durante $ T '$ dalla parte anteriore al punto di incontro $ fL $ è $$ cT' = fL - vT '\ tag {3}. $$ Dall'equazione (1), troviamo $$ \ frac {T '} {T} = \ frac {cw} {c + w} \ tag {4}, $$ e combinando questo con (2) e (3), troviamo $$ f = \ left (\ frac {c + v} {cv} \ right) \ frac {T '} {T} = \ frac {(c + v) (cw)} {(cv) (c + w)}. \ tag { 5} $$ Poiché $ f $ è invariante, questa relazione rimane vera nel sistema di riferimento $ S '$ che si muove con il treno. In questo frame, $ v = 0 $ e la particella massiccia avrà una velocità diversa, diciamo $ u $. Quindi otteniamo $$ f = \ frac {c-u} {c + u}. \ Tag {6} $$ Se ora identifichiamo (5) e (6), troviamo $$ \ frac {c + w} {cw} = \ left (\ frac {c + u} {cu} \ right) \ left (\ frac {c + v} {cv} \ right), \ tag {7} $$ e la risoluzione di $ w $ porta alla familiare legge di addizione relativistica: $$ w = \ frac {u + v} {1 + uv / c ^ 2 }. \ tag {8} $$ Le uniche ipotesi in questo semplice esperimento mentale sono che la velocità della luce $ c $ e i rapporti tra le lunghezze siano invarianti.