Tuttavia, se $ H $ è definito come una funzione di $ q, p, t $ span>, allora come possiamo definire $ H (q, p, t) = \ dot q * p - L (q, \ dot q, t) $ , cioè $ \ dot q $ non è un argomento di $ H $ mentre è nella sua definizione.

Come al solito in una trasformazione di Legendre, l'espressione sopra per $ H $ dovrebbe essere intesa come una notazione abbreviata per $$ H (q, p, t) = \ punto q (q, p, t) \ cdot p-L (q, \ punto q (q, p, t), t) $$ dove $ \ dot q (q, p, t) $ si ottiene invertendo la definizione di $ p $ span> $$ p = \ frac {\ partial L} {\ partial \ dot q} (q, \ dot q, t) $$ per ottenere la funzione $ \ dot q (q, p, t) $ .

$ \ boldsymbol {\ S \:} \ textbf {A. In generale} $

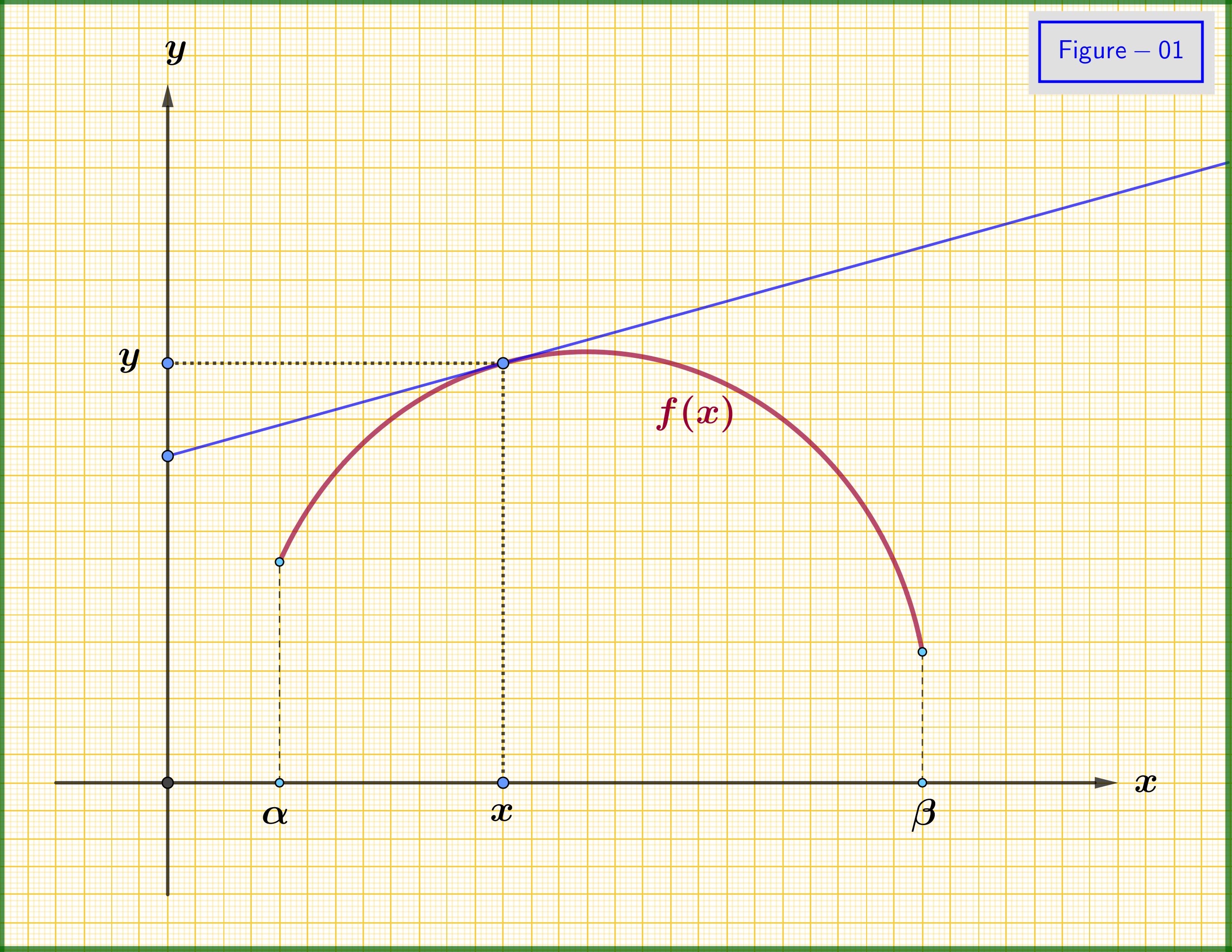
Considera una funzione reale $ \: f \ left (x \ right) \: $ di una variabile reale $ x \ in \ left [\ alpha, \ beta \ right] $ con derivate continue 1a e 2a. Supponiamo che la sua seconda derivata sia ovunque negativa in modo che il suo grafico nel piano $ \: xy- $ sia come nella Figura 01. Da ogni punto del grafico abbiamo una linea tangente.

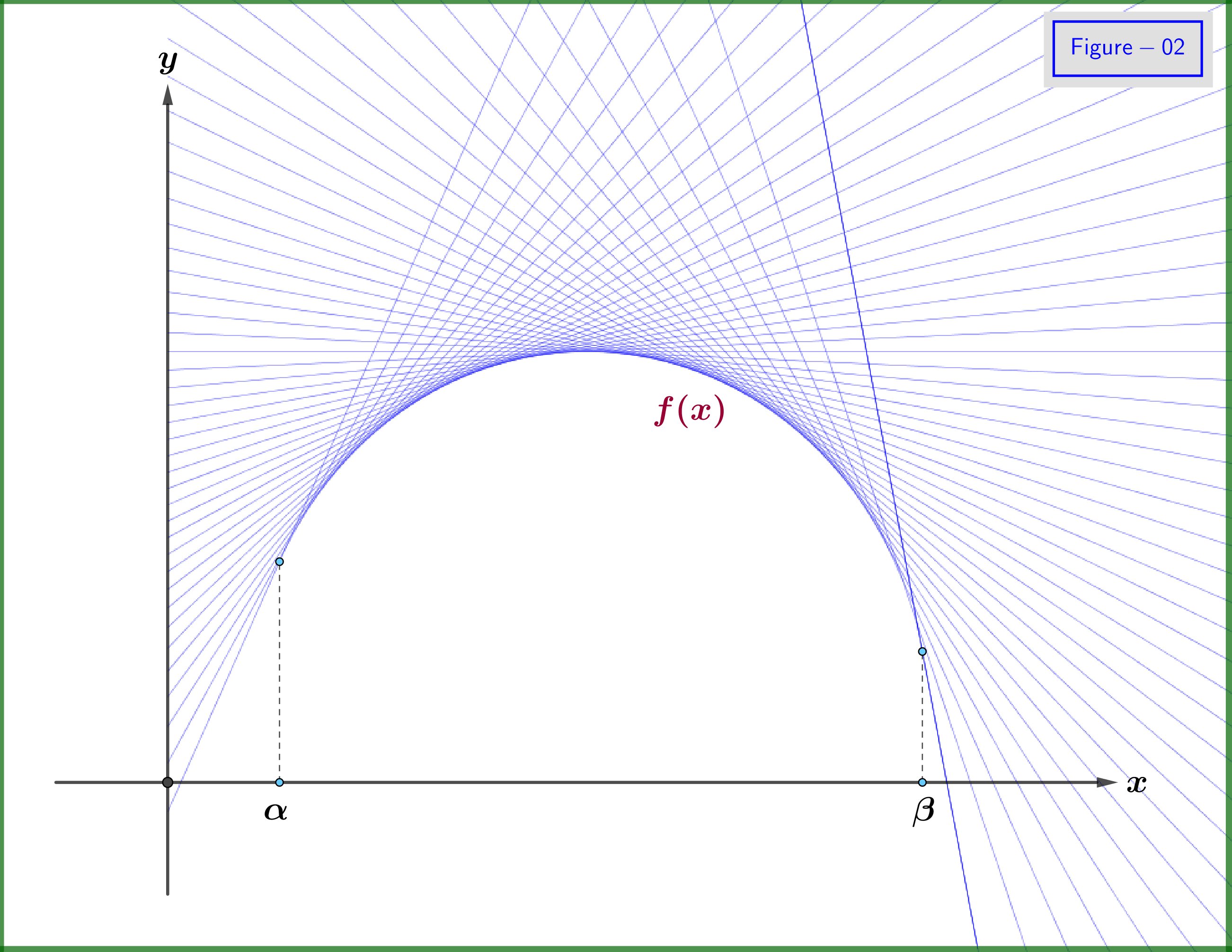
Ora, il grafico della funzione potrebbe essere tracciato dalla famiglia delle linee tangenti, vedere la Figura 02. Diciamo che questa curva (grafico) è l ' inviluppo della famiglia delle linee tangenti. Da questo fatto notiamo che potremmo definire la funzione $ \: f \ left (x \ right) \: $ dalla famiglia delle sue linee tangenti. Infatti, come mostrato nella Figura 03, se dall'angolo $ \: \ theta \: $ di una qualsiasi linea tangente, conosciamo il punto in cui questa linea interseca la $ \: y- $ asse, lascia che $ \: \ boldsymbol {-} \ omega \: $ (il segno meno utilizzato per scopi futuri), avremmo una definizione equivalente della funzione $ \: f \ left (x \ right) $ . Quindi, dobbiamo avere la funzione $ \: \ omega \ left (\ theta \ right) $ . Per il dominio dell'angolo $ \: \ theta \: $ abbiamo come esempio dalla Figura 03

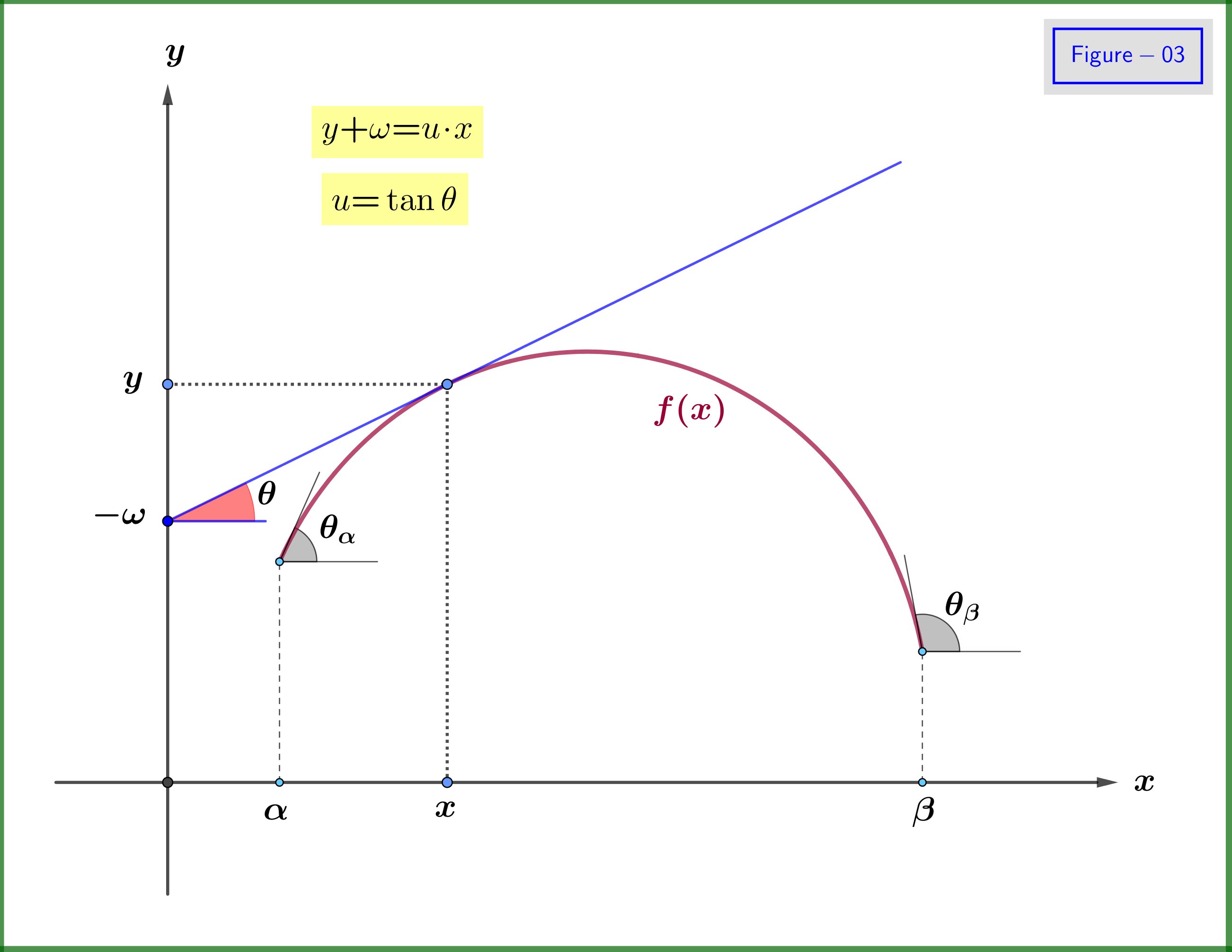
\ begin {equation} \ theta \ in \ left [\ theta_1, \ theta_2 \ right] \ quad \ text {dove} \ quad \ theta_1 \ boldsymbol {=} \ min {(\ theta_ \ alpha, \ theta_ \ beta)} \ quad \ text {e} \ quad \ theta_2 \ boldsymbol {=} \ max {(\ theta_ \ alpha, \ theta_ \ beta)} \ tag {A-01} \ label {A-01} \ end {equation}

Invece di utilizzare l'angolo $ \: \ theta \: $ utilizziamo ugualmente bene la variabile $ \: u \ boldsymbol {=} \ tan \ theta \ boldsymbol {=} \ dfrac {\ mathrm df} {\ mathrm dx} $ . Per il dominio di $ \: u \: $ abbiamo
\ begin {equation} u \ in \ left [u_1, u_2 \ right] \ quad \ text {dove} \ quad u_1 \ boldsymbol {=} \ min {(\ tan \ theta_ \ alpha, \ tan \ theta_ \ beta)} \ quad \ text {e} \ quad u_2 \ boldsymbol {=} \ max {(\ tan \ theta_ \ alpha, \ tan \ theta_ \ beta)} \ tag {A-02} \ label {A-02} \ end {equation}

Dalla Figura 03 abbiamo \ begin {equation} y \ boldsymbol {+} \ omega \ boldsymbol {=} \ tan \ theta \ cdot x \ boldsymbol {=} u \ cdot x \ tag {A-03} \ label {A-03} \ end {equation} così \ begin {equation} \ boxed {\: \: \ omega \ left (u \ right) \ boldsymbol {=} u \ cdot x \ boldsymbol {-} f \ left (x \ right) \ vphantom {\ dfrac {a} {b}} \: \:} \ tag {A-04} \ label {A-04} \ end {equation} Ora guardando nell'equazione sopra sembra matematicamente illogico l'argomento che la funzione $ \: \ omega \: $ non dipenda dalla variabile $ \: x \: $ e dobbiamo scrivere \ begin {equation} \ omega \ left (u, x \ right) \ stackrel {???} {\ boldsymbol {=}} u \ cdot x \ boldsymbol {-} f \ left (x \ right) \ tag {A-05} \ label {A-05} \ end {equation} Ma qui non è questo il caso perché da \ eqref {A-04} \ begin {equation} \ dfrac {\ partial \ omega} {\ partial x} \ boldsymbol {=} u \ boldsymbol {-} \ dfrac {\ partial f} {\ partial x} \ boldsymbol {=} \ dfrac {\ mathrm df} {\ mathrm dx} \ boldsymbol {-} \ dfrac {\ mathrm df} {\ mathrm dx} \ boldsymbol {=} 0 \ tag {A-06} \ label {A-06} \ end {equation} cioè $ \: \ omega \: $ è indipendente da $ \: x $ . Dipende solo da $ \: u \: $ ecco perché scriviamo $ \: \ omega \ left (u \ right ) $ .

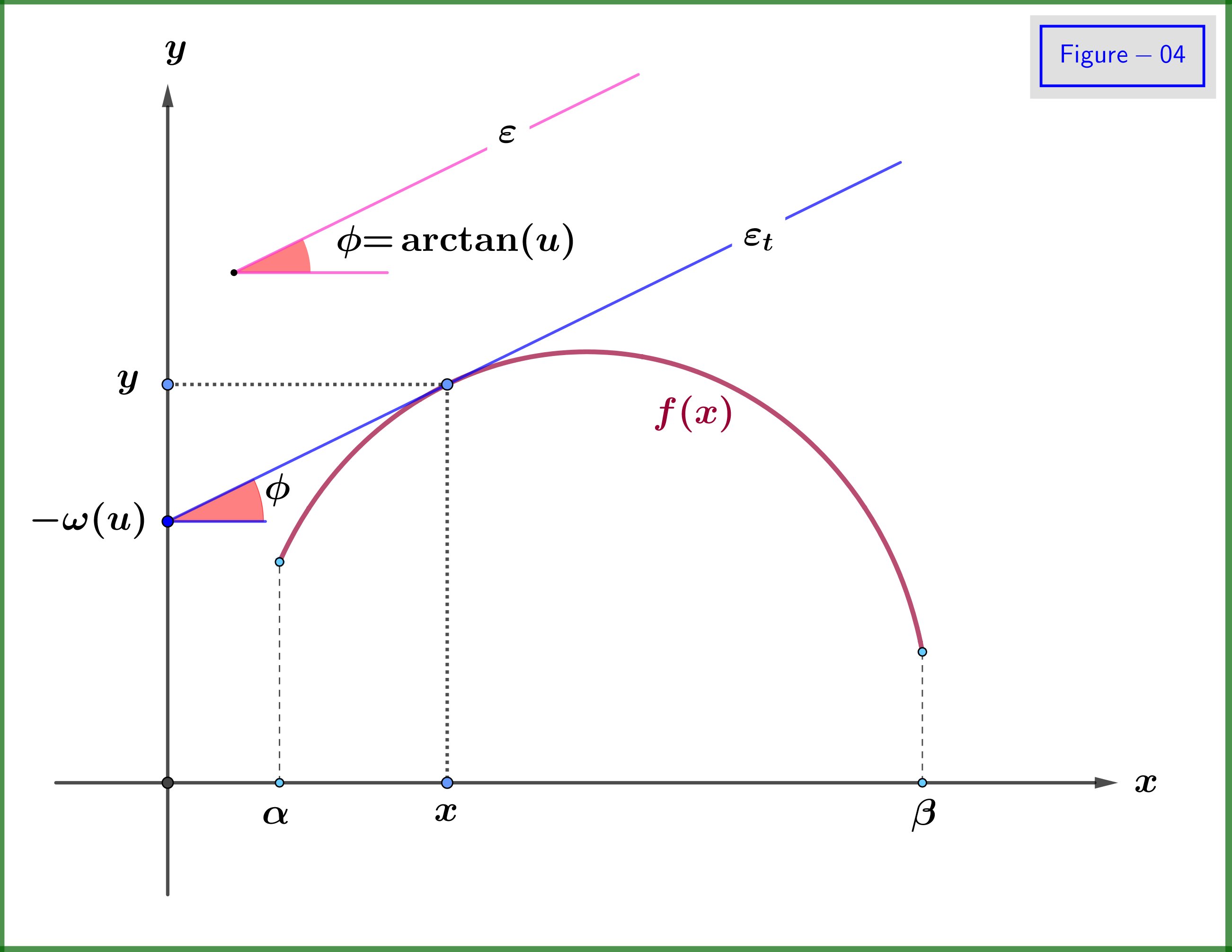
Nella Figura 04 questo fatto è spiegato graficamente: supponiamo che un valore $ \: u \ in \ left [u_1, u_2 \ right] \: $ sia dato. È come dare una direzione, ovvero una linea $ \: \ varepsilon \: $ con un angolo $ \: \ phi \ boldsymbol {=} \ arctan (u) $ . Troviamo una linea univoca $ \: \ varepsilon_t \: $ tangente al grafico della curva di $ \: f \ left (x \ right) \: $ e parallelo a $ \: \ varepsilon \: $ che interseca il $ \: y- $ asse in $ \: \ boldsymbol {-} \ omega (u) $ . Oltre il valore della variabile indipendente $ \: u \: $ non è necessario alcun valore di $ \: x $ . Al contrario, questo valore di $ \: x \: $ è determinato automaticamente sottoterra dal punto di contatto della linea tangente $ \: \ varepsilon_t \: $ con il grafico.

Chiamiamo la funzione $ \: \ omega \ left (u \ right) \: $ Legendre transform della funzione $ \: f \ left (x \ right) \: $ rispetto alla variabile $ \: x $ .

Nota che differenziando \ eqref {A-04} rispetto a $ \: u \: $ abbiamo \ begin {equation} x \ boldsymbol {=} \ dfrac {\ mathrm d \ omega \ left (u \ right)} {\ mathrm du} \ tag {A-07} \ label {A-07} \ end {equation} Quindi, la funzione $ \: f \ left (x \ right) \: $ e la sua trasformazione Legendre rispetto a $ \: x \: $ , ovvero la funzione $ \: \ omega \ left (u \ right) $ , soddisfa il seguente insieme di equazioni \ begin {align} f \ left (x \ right) \ boldsymbol {+} \ omega \ left (u \ right) & \ boldsymbol {=} u \ cdot x \ tag {A-08a} \ label {A-08a} \\ u & \ boldsymbol {=} \ dfrac {\ mathrm df \ left (x \ right)} {\ mathrm dx} \ tag {A-08b} \ label {A-08b} \\ x & \ boldsymbol {=} \ dfrac {\ mathrm d \ omega \ left (u \ right)} {\ mathrm du} \ tag {A-08c} \ label {A-08c} \ end {align}

Se nelle equazioni precedenti scambiamo i ruoli come segue \ begin {align} f & \ boldsymbol {\ rightleftarrows} \ omega \ tag {A-09a} \ label {A-09a} \\ x & \ boldsymbol {\ rightleftarrows} u \ tag {A-09b} \ label {A-09b} \ end {align} quindi le equazioni \ eqref {A-08a}, \ eqref {A-08b} e \ eqref {A-08c} danno rispettivamente \ begin {align} \ omega \ left (u \ right) \ boldsymbol {+} f \ left (x \ right) & \ boldsymbol {=} x \ cdot u \ tag {A-10a} \ label {A-10a} \\ x & \ boldsymbol {=} \ dfrac {\ mathrm d \ omega \ left (u \ right)} {\ mathrm du} \ tag {A-10b} \ label {A-10b} \\ u & \ boldsymbol {=} \ dfrac {\ mathrm df \ left (x \ right)} {\ mathrm dx} \ tag {A-10c} \ label {A-10c} \ end {align}

Ma questo insieme di equazioni è identico a quello di (A-08): la funzione $ \: f \ left (x \ right) \: $ è la trasformazione Legendre di $ \: \ omega \ left (u \ right) $ rispetto a $ \: u $ . Questa applicazione di due successive trasformazioni di Legendre restituisce la funzione iniziale.

$ \ boldsymbol {\ S \:} \ textbf {B. Meccanica classica - Funzioni di Lagrange e Hamilton} $

Nella meccanica classica l'equazione del moto di Eulero-Lagrange per un grado di libertà è \ begin {equation} \ dfrac {\ mathrm d} {\ mathrm dt} \ left (\ dfrac {\ partial L} {\ partial \ dot q} \ right) \ boldsymbol {-} \ dfrac {\ partial L} {\ partial q} \ grassetto {=} 0 \ tag {B-01} \ label {B-01} \ end {equation} dove \ begin {align} L \ left (q, \ dot q, t \ right) & \ boldsymbol {\ equiv} \ text {la funzione Lagrange} \ tag {B-02a} \ label {B-02a} \\ q & \ boldsymbol {\ equiv} \ text {la coordinata generalizzata} \ tag {B-02b} \ label {B-02b} \\ \ dot q & \ boldsymbol {\ equiv} \ dfrac {\ mathrm d q} {\ mathrm d t} \ tag {B-02c} \ label {B-02c} \ end {align} Per la trasformata di Legendre della funzione Lagrange $ \: L \ left (q, \ dot q, t \ right) \: $ rispetto alla variabile indipendente $ \: \ dot q \: $ sostituiamo tutte le variabili, le funzioni e gli operatori differenziali in $ \: \ boldsymbol {\ S \ :} \ textbf {A} \: $ come segue \ begin {align} \ text {Variabili} \: \: \:: \: \: \: & \sinistra. \ begin {case} X\!\!\! & \! \! \! \ boldsymbol {- \! \! \! - \! \! \! - \! \! \! \ rightarrow} \ dot q \\ u \! \! \! & \! \! \! \ boldsymbol {- \! \! \! - \! \! \! - \! \! \! \ rightarrow} p \ end {case} \ right \} \ tag {B-03a} \ label {B-03a} \\ \ text {Funzioni} \: \: \:: \: \: \: & \sinistra. \ begin {case} f \! \! \! & \! \! \! \ boldsymbol {- \! \! \! - \! \! \! - \! \! \! \ rightarrow} L \\ \omega\!\!\! & \! \! \! \ boldsymbol {- \! \! \! - \! \! \! - \! \! \! \ rightarrow} H \ end {case} \ right \} \ tag {B-03b} \ label {B-03b} \\ \ text {Operatori} \: \: \:: \: \: \: & \sinistra. \ begin {case} \ dfrac {\ mathrm d \ hphantom {x}} {\ mathrm d x} \! \! \! & \! \! \! \ boldsymbol {- \! \! \! - \! \! \! - \! \! \! \ rightarrow} \ dfrac {\ partial \ hphantom {x}} {\ partial \ dot q} \ vphantom {\ dfrac {a} {\ dfrac {a} {b}}} \\ \ dfrac {\ mathrm d \ hphantom {u}} {\ mathrm d u} \! \! \! & \! \! \! \ boldsymbol {- \! \! \! - \! \! \! - \! \! \! \ rightarrow} \ dfrac {\ partial \ hphantom {p}} {\ partial p} \ end {case} \ right \} \ tag {B-03c} \ label {B-03c} \ end {align} Le equazioni \ eqref {A-08a}, \ eqref {A-08b} e \ eqref {A-08c} danno rispettivamente \ begin {align} H \ sinistra (q, p, t \ destra) \ boldsymbol {+} L \ left (q, \ dot q, t \ right) & \ boldsymbol {=} p \, \ dot q \ tag {B-04a} \ label {B-04a} \\ p & \ boldsymbol {=} \ dfrac {\ partial L \ left (q, \ dot q, t \ right)} {\ partial \ dot q} \ tag {B-04b} \ label {B-04b} \\ \ dot q & \ boldsymbol {=} \ dfrac {\ partial H \ left (q, p, t \ right)} {\ partial p} \ tag {B-04c} \ label {B-04c} \ end {align} Quindi la trasformata di Legendre della funzione Lagrange $ \: L \ left (q, \ dot q, t \ right) \: $ rispetto alla variabile indipendente $ \: \ dot q \: $ è la funzione Hamilton $ \: H \ left (q, p, t \ right) \: $ , da dove \ eqref {B-04a} \ begin {equation} H \ sinistra (q, p, t \ destra) \ boldsymbol {=} p \, \ dot q \ boldsymbol {-} L \ left (q, \ dot q, t \ right) \ tag {B-05} \ label {B-05} \ end {equation} Nello spirito della discussione in $ \: \ boldsymbol {\ S \:} \ textbf {A} \: $ la funzione Hamilton $ \: H \ left (q, p, t \ right) \: $ è indipendente dalla variabile $ \: \ dot q $ span >, dipende dalla variabile indipendente $ \: p \ boldsymbol {\ equiv} \ text {the generalized momentum} $ .

L'equazione \ eqref {B-05} restituisce \ begin {equation} \ dfrac {\ partial H \ left (q, p, t \ right)} {\ partial q} \ boldsymbol {=} \ boldsymbol {-} \ dfrac {\ partial L \ left (q, \ dot q, t \ destra)} {\ partial q} \ tag {B-06} \ label {B-06} \ end {equation} Da questa equazione e dalla definizione di $ \: p $ , vedere l'equazione \ eqref {B-04b}, l'equazione del moto di Eulero-Lagrange \ eqref {B-01} dà \ begin {equation} \ dot p \ boldsymbol {=} \ boldsymbol {-} \ dfrac {\ partial H \ left (q, p, t \ right)} {\ partial q} \ tag {B-07} \ label {B-07} \ end {equation} Le equazioni \ eqref {B-04c} e \ eqref {B-07} costituiscono insieme le equazioni del moto di Hamilton \ begin {equation} \ text {Equazioni del moto di Hamilton} \: \: \:: \: \: \: \sinistra. \ begin {case} \ dot q & \! \! \ boldsymbol {=} \ boldsymbol {+} \ dfrac {\ partial H \ left (q, p, t \ right)} {\ partial p} \ vphantom {\ dfrac {a} {\ dfrac {a} {b}}} \\ \ dot p & \! \! \ boldsymbol {=} \ boldsymbol {-} \ dfrac {\ partial H \ left (q, p, t \ right)} {\ partial q} \ end {case} \ right \} \ tag {B-08} \ label {B-08} \ end {equation}

La formula fornita da Goldstein (8.15) non è una definizione dell'hamiltoniano (poiché hai ragione, la formula dipende da $ \ dot {q} $ span >, che non è un argomento dell'Hamiltoniano. Tuttavia, la formla può essere intesa come un'equazione che vogliamo $ H $ per soddisfare se la variabile $ p $ soddisfa \ begin {align} p = \ frac {\ partial L} {\ partial \ dot {q}} (q, \ dot {q}, t) \ end {align}

A differenza di quanto suggerito nella versione precedente di questa risposta, $ p $ , $ q $ e $ \ dot {q} $ possono essere variabili indipendenti in queste equazioni.

Ormai è anche chiaro perché $ p \ dot {q} $ scompare qui: il differenziale del termine $ \ dot {q} p $ nella formula 8.15 annulla con quello dal differenziale di $ L $ in 8.13.

Scritto: \ begin {align} dH = d \ punto {q} p - \ punto {q} dp - dL \ end {align}
Con $ dL $ da 8.13, arrivi alla stessa formula a cui arriva Goldstein.

Nota importante da parte mia: Goldstein discute con la trasformazione di Legendre qui quando parla del motivo per cui il differenziale svanisce. In effetti, il modo in cui ha "definito" $ H $ è una trasformazione di Legendre. Tuttavia, poiché ha iniziato a definire $ H $ senza usare il termine "Legendre-Transform", avrebbe potuto discutere senza di esso anche in seguito parlando del differenziali. Come ho fatto io, puoi perfettamente capire perché $ d \ dot {q} p $ svanisce senza usare il termine "Legendre-Transformation".Al contrario, quando Goldstein scrive che $ d \ dot {q} p $ svanisce a causa della "Legendre-Transformation", significa implicitamente esattamente quello che ho scritto.

Bene, $ \ dot {q} $ non è un documento di $ H $ e di telo vedrà solo in seguito, ma è una funzione del tempo quindi devi fare $ dH $ dalla definizione (8.15) tenendolo a mente e devi usare $ dL $ da (8.13 ').Poi arrivi al giusto differenziale hamiltoniano.Nota, eq.(8.16) manca un fattore $ dt $ nell'ultimo termine (un errore di battitura).

Per prima cosa proviamo la trasformazione legendre su un particolare esempio.

$$ L = \ frac12 m \ dot {q} ^ 2 - V (q), $$

secondo Goldstein l'hamiltoniana per questo sistema è,

$$ H = \ dot {q} p - L, $$

inizialmente pensiamo a $ p $ e $ \ dot {q} $ come variabili indipendenti . Se prendiamo $ \ partial H / \ partial \ dot {q} $ otterremo,

$$ \ frac {\ partial H} {\ partial \ dot {q}} = p - \ frac {\ partial L} {\ partial \ dot {q}} , $$

se ora ci limitiamo alla superficie $ p = \ frac {\ partial L} {\ partial \ dot {q}} $ troviamo che la derivata di $ H $ rispetto a $ \ dot {q} $ svanisce.

Ai fini del calcolo delle dinamiche, vincoleremmo i nostri risultati,

$$ H \ Big | _ {p = m \ dot {q}} = \ Big (p \ dot {q} - L (\ dot {q}, q ) \ Big) \ Big | _ {p = m \ dot {q}} $$

$$ H \ Big | _ {p = m \ dot {q}} = \ Big (\ frac {p ^ 2} {m} - L (p / m , q) \ Big) \ Big | _ {p = m \ dot {q}} $$

$$ H \ Big | _ {p = m \ dot {q}} = \ Big (\ frac {p ^ 2} {m} - \ frac {p ^ 2} {2 m} + V (q) \ Big) \ Big | _ {p = m \ dot {q}} $$

$$ H \ Big | _ {p = m \ dot {q}} = \ Big (\ frac {p ^ 2} {2m} + V (q) \ Big) \ Big | _ {p = m \ dot {q}} $$

Questo tipo di pratica del "vincolare le nostre variabili dopo il fatto" è molto comune nella meccanica classica.