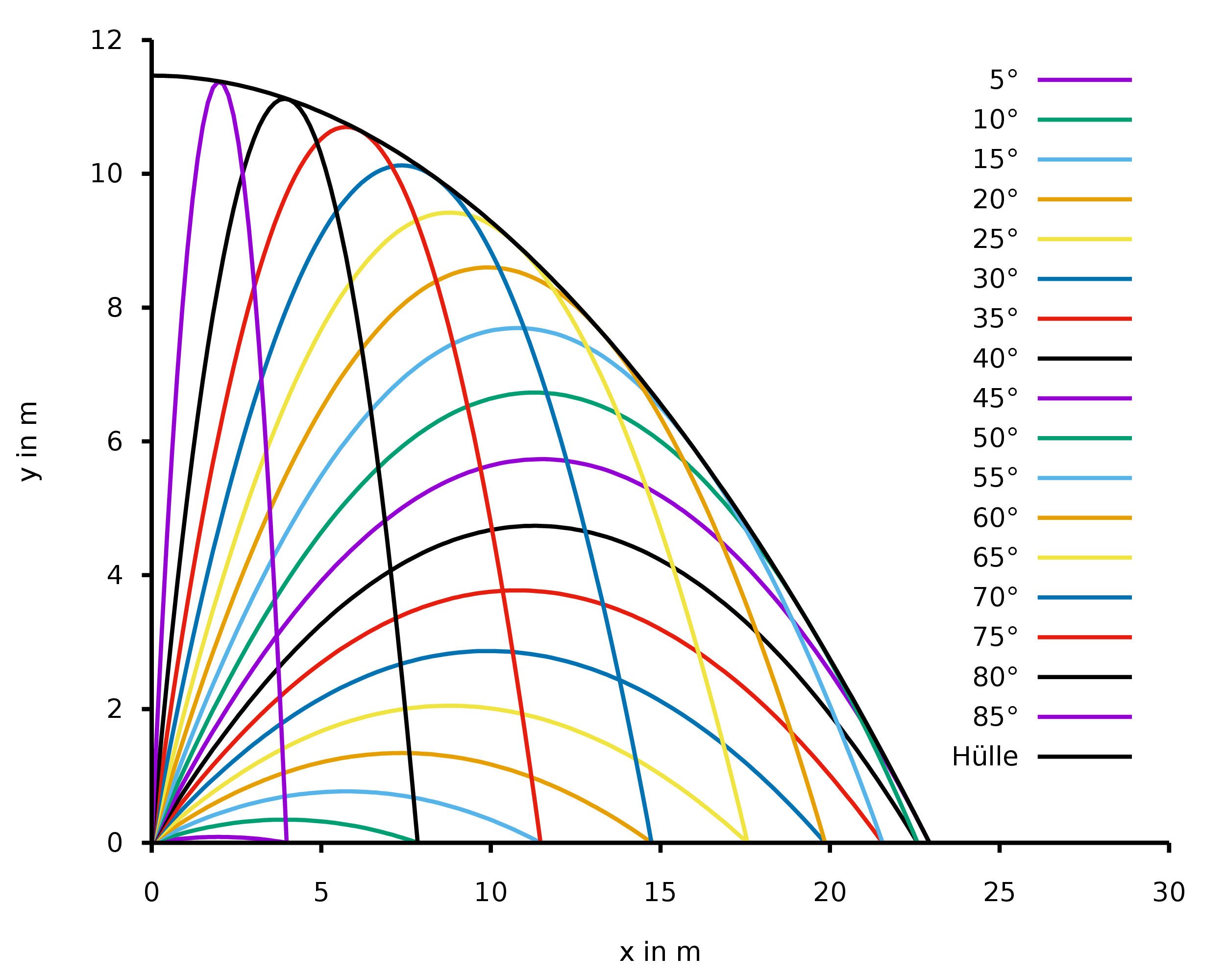
Ciascuna delle particelle d'acqua viene spinta di lato dalle altre particelle quando l'acqua colpisce il muro. Se trascuriamo la viscosità dell'acqua, ciascuna di queste particelle segue una parabola di lancio, ma con angoli di lancio iniziali diversi. Se assumiamo che il getto colpisca il muro orizzontalmente, le particelle d'acqua vengono lanciate con la stessa velocità iniziale (massima) in ogni direzione. La forma che hai osservato è quindi data dall'involucro di tutte le possibili parabole.

Per tutte le parabole $$ y (x) = x \ tan \ beta - \ frac {g \, x ^ 2} {2 \, {v_0} ^ 2 \ cos ^ 2 \ beta} + h_0 $$ con angoli di lancio iniziali $ \ beta $ , la busta è $$ y_ \ mathrm {H} (x) = \ frac {{v_0} ^ 2} {2 \, g} - \ frac {g \, x ^ 2} {2 \, {v_0} ^ 2} + h_0. $$

Quindi forma davvero una parabola.

Modifica: la busta può essere derivata come segue:

Se definiamo la famiglia di curve implicitamente da $$ F (x, y, \ tan (\ beta)) = y - x \ tan \ beta + \ frac {g \, x ^ 2} {2 \, {v_0 } ^ 2 \ cos ^ 2 \ beta} = y - x \ tan \ beta + \ frac {g \, x ^ 2 (1+ \ tan ^ 2 \ beta)} {2 \, {v_0} ^ 2} = 0 $$ la busta della famiglia è data da ( Fonte) $$ F = 0 ~~ \ mathsf {e} ~~ {\ partial F \ over \ partial \ tan \ beta} = 0 $$ abbiamo $$ {\ partial F \ over \ partial \ tan \ beta} = - x + \ frac {gx ^ 2 \ tan \ beta} {v_0 ^ 2} = 0 ~~ \ Leftrightarrow ~~ \ tan \ beta = \ frac {v_0 ^ 2} {gx} $$ Sostituendolo in $ F $ otteniamo $$ F = y- \ frac {v_0 ^ 2} {g} + \ frac {g (x ^ 2 + v_0 ^ 4 / g ^ 2)} {2v_0 ^ 2} = 0 ~~ \ Leftrightarrow ~~ y_ \ mathrm {H} (x) = \ frac {{v_0} ^ 2} {2 \, g} - \ frac {g \, x ^ 2} {2 \, {v_0 } ^ 2} $$

Se il getto d'acqua colpisce la superficie orizzontale , il liquido scorre via in un flusso laminare a film sottile fino a quando il flusso diventa più lento e turbolento a una certa distanza dal punto della zona di conflitto in un cerchio salto idraulico. Se la superficie su cui urta il getto è verticale, questo salto idraulico forma una “fune” che scorre circonferenzialmente attorno alla regione di flusso laminare radiale. La fisica del flusso è piuttosto complicata, combinando la transizione del flusso laminare con quello turbolento, la viscosità di taglio, la tensione superficiale, la gravità e l'interazione del fluido con la parete, quindi non ci sarebbe una soluzione semplice. Tuttavia, questa situazione fisica ha un'importanza pratica e quindi è stata studiata sperimentalmente:

Quindi ecco un paio di documenti dedicati a questo argomento, l'immagine sopra è tratta dal primo:

• Wang, T., Faria, D., Stevens, L. J., Tan, J. S. C., Davidson, J. F., & Wilson, D. I. (2013). Schemi di flusso e film drenanti creati da getti d'acqua coerenti orizzontali e inclinati che colpiscono le pareti verticali . Chemical Engineering Science, 102, 585-601, doi: 10.1016 / j.ces.2013.08.054.

• Aouad, W., Landel, J. R., Dalziel, S. B., Davidson, J. F., & Wilson, D. I. (2016). Velocimetria delle immagini delle particelle e modellazione di getti di liquido coerenti orizzontali che colpiscono e drenano una parete verticale . Experimental Thermal and Fluid Science, 74, 429-443, doi: 10.1016 / j.expthermflusci.2015.12.010, pdf gratuito.

Perché se non ci fosse la gravità ad influire, l'acqua si diffonderebbe anche orizzontalmente, ma a causa dell'effetto della gravità la diffusione orizzontale viene "trascinata" verso il basso rispetto al punto di impatto iniziale.