I) Ci sono già molte buone risposte. OP sta chiedendo lo momento della stringa non relativistica con solo spostamenti trasversali, la cui densità lagrangiana di solito è data come
$$ {\ cal L} _T ~: = ~ \ frac {\ rho} {2} \ dot {\ eta} ^ 2 - \ frac {\ tau} { 2} \ eta ^ {\ prime 2} \ tag {1} $$
nei libri di testo.
II) Fissiamo la notazione: $ \ rho $ è la densità di massa 1D; $ \ tau $ è la tensione della stringa; $ Y $ è il modulo di Young 1D; il punto indica una derivata rispetto a. $ x ^ 0 \ equiv t $ ; prime denota una derivata rispetto a. $ x ^ 1 \ equiv x $ ; $ \ xi $ è lo spostamento longitudinale nella direzione $ x $ ; e $ \ eta $ è lo spostamento trasversale nella $ y $ -direzione.
III) Prima di tutto, nota che il tensore canonico stress-energia-momento (SEM) $ T ^ {\ mu} {} _ { \ nu} $ (che contiene la densità di momento $ T ^ 0 {} _ 1 $ ) è un pull-back to the world sheet (WS), che identifichiamo con il $ (x, t) $ -piano. Pertanto la direzione della quantità di moto è spesso identificata con la direzione $ x $ longitudinale, anche se le vibrazioni dello spazio bersaglio fisico (TS) sono nella $ y $ -direction.
In secondo luogo, si noti che già per il modello a onde longitudinali (concettualmente più semplice)
$$ {\ cal L} _L ~: = ~ \ frac {\ rho} {2} \ dot {\ xi} ^ 2 - \ frac {Y} {2 } \ xi ^ {\ prime 2}, \ tag {2} $$
(meno) la densità di quantità di moto canonica
$$ T ^ 0 {} _ 1 ~ = ~ \ rho \ dot {\ xi} \ xi ^ {\ prime} \ tag {3} $$
è diverso dalla densità di momento cinetico $ \ rho \ dot {\ xi} $ . Ciò è legato al fatto che il modello (2) è costruito per descrivere le eccitazioni d'onda della stringa, non le sue traslazioni complessive. Il messaggio da portare via è che non è necessariamente una cosa utile cercare di rendere uguale lo slancio canonico e lo slancio cinetico. (E in particolare, il Rif. 1 non raggiunge questo obiettivo. Inoltre, il Rif. 1 discute solo delle eccitazioni chirali, cioè un motore sinistro o destro, ma non una sua sovrapposizione, che è incompleta per una teoria non lineare. )
Basti dire che i diversi momenti possono essere trattati e compresi separatamente e che esistono leggi di conservazione associate a entrambi i tipi di momenti. La conservazione della quantità di moto cinetica deriva dalle leggi di Newton, mentre la conservazione della quantità di moto canonica è una conseguenza della simmetria di traslazione, cfr. Teorema di Noether. In questa risposta, ci concentreremo sull'ottenere un modello fisico più realistico dell'onda trasversale rispetto alla densità lagrangiana (1).
IV) Il nostro punto di partenza è la semplice osservazione che per una stringa non estensibile $ Y \ gg \ tau $ , un piccolo spostamento trasversale
$$ \ eta ~ = ~ {\ cal O} (\ varepsilon), \ tag {4} $$
dove $ \ varepsilon \ ll 1 $ , deve essere accompagnato da uno spostamento longitudinale
$$ \ xi ~ = ~ {\ cal O} (\ varepsilon ^ 2), \ tag {5} $$
cfr. Fig. 1 di seguito.
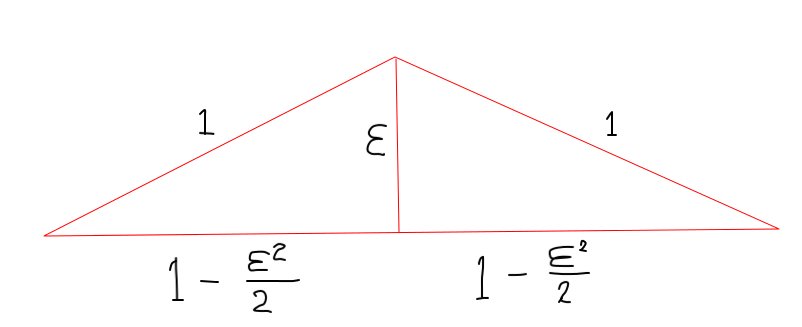
$ \ uparrow $ Fig. 1. Uno spostamento trasversale infinitesimale a dente di sega $ \ varepsilon \ ll 1 $ span > di una stringa non estensibile deve essere accompagnato da uno spostamento longitudinale $ \ frac {\ varepsilon ^ 2} {2} $ .
V) Concludiamo che un modello realistico per le eccitazioni trasversali $ \ eta $ deve includere la possibilità di spostamenti longitudinali $ anche \ xi $ . Consideriamo quindi la densità lagrangiana
$$ {\ cal L} ~: = ~ {\ cal T} - {\ cal V}, \ qquad
{\ cal T} ~: = ~ \ frac {\ rho} {2} \ left (\ dot {\ xi} ^ 2 + \ dot {\ eta} ^ 2 \ right), \ tag {6} $$
dove la densità potenziale $ {\ cal V} $ dovrebbe essere data dalla legge di Hooke. Lascia
$$ s ^ {\ prime} ~ = ~ \ sqrt {(1+ \ xi ^ {\ prime}) ^ 2 + \ eta ^ {\ prime 2}}
~ = ~ 1 + \ xi ^ {\ prime} + \ frac {\ eta ^ {\ prime 2}} {2} - \ frac {\ xi ^ {\ prime} \ eta ^ {\ prime 2}} {2 } - \ frac {\ eta ^ {\ prime 4}} {8} + {\ cal O} (\ varepsilon ^ 5) \ tag {7} $$
essere la derivata della lunghezza dell'arco $ s $ wrt. il $ x $ -coordinate. Modulo possibili termini derivati totali, la densità potenziale $ {\ cal V} $ deve essere nella forma
$$ {\ cal V} ~ = ~ \ frac {k} {2} \ left (s ^ {\ prime} -a \ right) ^ 2
~ = ~ \ frac {k} {2} (s ^ {\ prime} -1) ^ 2 + k (1-a) (s ^ {\ prime} -1) + \ frac {k} {2} ( 1-a) ^ 2 \ tag {8} $$
per le costanti del materiale adatte $ k $ e $ a $ , cf. Rif. 1. Come risulterà evidente di seguito, dovremmo identificare le due costanti $ k $ e $ a $ come
$$ k ~ = ~ Y + \ tau \ quad \ text {e} \ quad \ tau ~ = ~ k (1-a). \ tag {9} $$
Pertanto la densità potenziale (8) diventa
$$ {\ cal V} ~ \ stackrel {(8) + (9)} {=} ~ \ frac {Y + \ tau} {2} (s ^ { \ prime} -1) ^ 2 + \ tau (s ^ {\ prime} -1) + \ frac {\ tau ^ 2} {2 (Y + \ tau)} $$
$$ ~ \ stackrel {(7)} {=} ~ \ tau \ left (\ xi ^ {\ prime} + \ frac {\ eta ^ {\ prime 2}} { 2} + \ frac {\ xi ^ {\ prime 2}} {2} \ right) + \ frac {Y} {2} \ left (\ xi ^ {\ prime} + \ frac {\ eta ^ {\ prime 2}} {2} \ right) ^ 2 + {\ cal O} (\ varepsilon ^ 5) + \ frac {\ tau ^ 2} {2 (Y + \ tau)}. \ Tag {10} $$ span>
Mantenendo solo i termini in ordine quartico e scartando i termini derivati totali e i termini costanti, la densità potenziale si legge
$$ {\ cal V} _4 ~: = ~ \ frac {\ tau} {2} \ left (\ xi ^ {\ prime 2} + \ eta ^ { \ prime 2} \ right) + \ frac {Y} {2} \ chi ^ 2, \ tag {11} $$
dove abbiamo definito la notazione abbreviata
$$ \ chi ~: = ~ \ xi ^ {\ prime} + \ frac {\ eta ^ {\ prime 2}} {2}. \ tag {12} $$
Il potenziale quartico (11) è sorprendentemente semplice. Per una stringa non estensibile $ Y \ gg \ tau $ , la riconosciamo nell'eq. (11) il vincolo
$$ \ chi ~ \ approx ~ 0, \ tag {13} $$
che è al centro della Fig. 1. Il vincolo (13) implica che un'eccitazione trasversale (4) al primo ordine in $ \ varepsilon $ induce un'eccitazione longitudinale (5) al secondo ordine in $ \ varepsilon $ . Come vedremo più avanti, anche una stringa estensibile ha un'affinità per il vincolo (13).
VI) Per inciso, possiamo riscrivere il potenziale quartico (11) come potenziale cubico
$$ {\ cal V} _3 ~: = ~ \ frac {\ tau} {2} \ left (\ xi ^ {\ prime 2} + \ eta ^ { \ prime 2} \ right) - \ frac {B ^ 2} {2Y} + B \ chi, \ tag {14} $$
dove $ B $ è un campo ausiliario. L ' equazione di Eulero-Lagrange (EL) per $ B $ è
$$ B ~ \ approx ~ Y \ chi. \ tag {15} $$
Le equazioni EL per $ \ xi $ e $ \ eta $ leggere
$$ \ rho \ ddot {\ xi} ~ \ stackrel {(14)} {\ approx} ~
\ tau \ xi ^ {\ prime \ prime} + B ^ {\ prime}
~ \ stackrel {(12) + (15)} {\ approx} ~ (\ tau + Y) \ xi ^ {\ prime \ prime}
+ Y \ eta ^ {\ prime} \ eta ^ {\ prime \ prime}, \ tag {16} $$
$$ \ rho \ ddot {\ eta} ~ \ stackrel {(14)} {\ approx} ~
\ tau \ eta ^ {\ prime \ prime} + \ sinistra (B \ eta ^ {\ prime} \ destra) ^ {\ prime}
~ \ stackrel {(12) + (15)} {\ approx} ~
\ tau \ eta ^ {\ prime \ prime} + \ frac {3Y} {2} \ eta ^ {\ prime 2} \ eta ^ {\ prime \ prime} + Y (\ xi ^ {\ prime} \ eta ^ {\ prime}) ^ {\ prime}, \ tag {17} $$
rispettivamente.
VII) Se integriamo il campo $ B $ nel potenziale cubico (14),
$$ {\ cal V} _3 \ quad \ stackrel {B} {\ longrightarrow} \ quad {\ cal V} _4, \ tag {18} $$ span>
recuperiamo il potenziale quartico (11). Le equazioni EL (16) & (17) diventano
$$ \ Box_L \ xi ~: = ~ \ ddot {\ xi} - c_L ^ 2 \ xi ^ {\ prime \ prime}
~ \ approx ~ \ frac {Y} {\ rho} \ eta ^ {\ prime} \ eta ^ {\ prime \ prime}
~ = ~ (c_L ^ 2-c_M ^ 2) \ eta ^ {\ prime} \ eta ^ {\ prime \ prime}, \ tag {19} $$
$$ \ Box_M \ eta ~: = ~ \ ddot {\ eta} - c_M ^ 2 \ eta ^ {\ prime \ prime}
~ \ approx ~ \ frac {Y} {\ rho} \ left (\ chi \ eta ^ {\ prime} \ right) ^ {\ prime}
~ = ~ (c_L ^ 2-c_M ^ 2) \ left (\ chi \ eta ^ {\ prime} \ right) ^ {\ prime}, \ tag {20} $$
dove abbiamo definito due velocità
$$ c_M ^ 2 ~: = ~ \ frac {\ tau} {\ rho} \ quad \ text {e} \ quad
c_L ^ 2 ~: = ~ \ frac {Y + \ tau} {\ rho}. \ tag {21} $$
Consideriamo solo le onde che si spostano a sinistra. Un'analisi semplice mostra che le equazioni EL (19) & (20) hanno due modalità di viaggio:
-
Un $ L $ -mode $ \ xi_L (x \! - \! c_Lt ) $ con $ \ eta_L (x \! - \! c_Lt) \ approx 0 $ (che viola formalmente il vincolo (13), ma ricorda l'eq . (5)).
-
Una modalità mista $ M $ $ \ xi_M (x \! - \! c_Mt) $ e $ \ eta_M (x \! - \! c_Mt) $ che soddisfa il vincolo $ \ chi_M (x \! - \! c_Mt) \ circa 0 $ nell'eq. (13).
VIII) Le due modalità di viaggio $ L $ e $ M $ sono indipendenti nel senso che possono attraversarsi l'un l'altro. Tuttavia la creazione (e l'annientamento) della modalità $ M $ non sono indipendenti dalla $ L $ -modalità. Il vincolo (13) ha un effetto sbilenco: uno spostamento trasversale è sempre associato a una retrazione longitudinale. Ricorda che se imponiamo condizioni al contorno di Dirichlet alle estremità spaziali della corda, non è possibile una retrazione longitudinale complessiva. La creazione (e l'annientamento) di una modalità $ M $ deve quindi stimolare una compensazione più rapida $ L $ -modalità che contrasta la componente longitudinale della modalità $ M $ . Vedi rif. 1 per ulteriori dettagli.
IX) Infine, è interessante provare a integrare il campo longitudinale $ \ xi $ nel modello quartico (11). Possiamo risolvere l'eq. (19) per il campo longitudinale
$$ \ xi ~ \ approx ~ \ frac {Y} {2 \ rho} \ int \! dt ^ {\ prime} dx ^ {\ prime} ~ G (x, t; x ^ {\ prime}, t ^ {\ prime}) \ frac {d} {dx ^ {\ prime}} \ eta ^ { \ prime} (x ^ {\ prime}, t ^ {\ prime}) ^ 2 $$
$$ ~ \ stackrel {\ text {int. per parti}} {=} ~ \ frac {Y} {2 \ rho} \ int \! dt ^ {\ prime} dx ^ {\ prime} \ left \ {- \ frac {d} {dx ^ {\ prime}} G (x, t; x ^ {\ prime}, t ^ {\ prime}) \ right \} \ eta ^ {\ prime} (x ^ {\ prime}, t ^ {\ prime}) ^ 2 \ tag {22} $$
introducendo una funzione di Green $ G (x, t; x ^ {\ prime}, t ^ {\ prime}) $ e light- coordinate del cono
$$ x ^ {\ pm} ~: = ~ t \ pm \ frac {x} {c_L}, \ qquad \ Delta x ^ {\ pm} ~: = ~ \ Delta t \ pm \ frac {\ Delta x} {c_L}, \ qquad \ Delta t ~: = ~ t - t ^ {\ prime}, \ qquad \ Delta x ~: = ~ x - x ^ {\ prime}. \ tag {23} $$
Quindi il D'Alembertiano in 1 + 1D diventa
$$ \ Box_L ~ = ~ 4 \ partial _ + \ partial _- \ tag {24}. $$
La funzione di Green $ G (x, t; x ^ {\ prime}, t ^ {\ prime}) $ soddisfa per definizione
$$ \ Box_L G (x, t; x ^ {\ prime}, t ^ {\ prime}) ~ = ~ \ delta (\ Delta t) \ delta ( \ Delta x) ~ = ~ \ frac {2} {c_L} \ delta (\ Delta x ^ +) \ delta (\ Delta x ^ -). \ Tag {25} $$
La funzione di Green ritardato è
$$ G _ {\ rm ret} (x, t; x ^ {\ prime}, t ^ {\ prime}) ~ = ~ \ frac {1} {2c_L } \ theta (\ Delta x ^ +) \ theta (\ Delta x ^ -). \ tag {26} $$
Tuttavia, per ottenere una formulazione lagrangiana (30) per la teoria quartica $ \ xi $ ridotta (11), dovremmo usare la funzione di Green simmetrizzata
$$ G (x, t; x ^ {\ prime}, t ^ {\ prime}) ~ = ~ \ frac {1} {2} G _ {\ rm ret} (x, t; x ^ {\ prime}, t ^ {\ prime}) + \ frac {1} {2} G _ {\ rm ret} (x ^ {\ prime}, t ^ {\ prime} ; x, t). \ tag {27} $$
È conveniente introdurre la notazione
$$ K (x, t; x ^ {\ prime}, t ^ {\ prime})
~: = ~ - \ frac {d} {dx} \ frac {d} {dx ^ {\ prime}} G (x, t; x ^ {\ prime}, t ^ {\ prime}) $$ span>
$$ ~ = ~ - \ frac {1} {4c_L} \ frac {d} {dx} \ frac {d} {dx ^ {\ prime}} \ left [\ theta (\ Delta x ^ +) \ theta (\ Delta x ^ -) + \ theta (- \ Delta x ^ +) \ theta (- \ Delta x ^ -) \ right] $$
$$ ~ = ~ - \ frac {1} {8c_L} \ frac {d} {dx} \ frac {d} {dx ^ {\ prime}} \ left [{\ rm sgn} (\ Delta x ^ +) {\ rm sgn} (\ Delta x ^ -) \ right]. \ tag {28} $$
Quindi la derivata $ \ xi ^ {\ prime} $ del campo longitudinale è data semplicemente da
$$ \ xi ^ {\ prime} (x, t) ~ \ approx ~ \ frac {Y} {2 \ rho} \ int \! dt ^ {\ prime} ~ dx ^ {\ prime} ~ K (x, t; x ^ {\ prime}, t ^ {\ prime}) ~ \ eta ^ {\ prime} (x ^ {\ prime}, t ^ {\ prime}) ^ 2. \ tag {29} $$
Infine, siamo in grado di scrivere un'azione
$$ \ begin {align} S_4 \ quad \ stackrel {\ xi} {\ longrightarrow} \ quad &
\ int \! dt ~ dx \ left (\ frac {\ rho} {2} \ dot {\ eta} ^ 2- \ frac {\ tau} {2} \ eta ^ {\ prime 2} - \ frac {Y} {8} \ eta ^ {\ prime 4} \ right) \ cr
&- \ frac {Y ^ 2} {8 \ rho} \ int dt ~ dx ~ dt ^ {\ prime} dx ^ {\ prime} ~ \ eta ^ {\ prime} (x, t) ^ 2 ~ K ( x, t; x ^ {\ prime}, t ^ {\ prime}) ~ \ eta ^ {\ prime} (x ^ {\ prime}, t ^ {\ prime}) ^ 2 \ end {align} \ tag {30} $$
per la teoria quartica $ \ xi $ ridotta (11). È facile verificare che l'equazione EL corrispondente per $ \ eta $ sia eq. (17), dove $ \ xi ^ {\ prime} $ sul lato destro dell'eq. (17) è dato dall'eq. (29).
L'azione (30) è bi-locale, come previsto. (Il lato positivo è che almeno l'azione (30) non dipende da derivati dello spaziotempo superiori!) Tuttavia la natura non locale sfida il concetto di un tensore SEM (e quindi la densità di momento canonica, che era ciò che OP aveva originariamente chiesto di). È ancora possibile derivare le leggi di conservazione di Noether associate alla simmetria di traduzione WS, ma non lo perseguiremo qui.
Riferimenti:
- D.R. Rowland & C. Pask, Il mistero dell'impeto dell'onda mancante, Am. J. Phys. 67 (1999) 378. (Punta di cappello: ACuriousMind.)