In genere considero la NASA autorevole e riportano i parametri orbitali sul loro Earth Fact Sheet. Noto che non sono d'accordo con Wikipedia sull'afelio sebbene siano d'accordo su perelio, semiasse maggiore ed eccentricità:

  NASA WikipediaAphelion 152.10 151.93Perhelion 147.09 147.095 Semi-major 149.60 149.598 Eccentricità 0.0167 0.0167086  

Poiché le cifre della NASA sono coerenti, presumo che ci sia un errore nella pagina di Wikipedia.

Esistono dati esatti sull'orbita terrestre?

No. Ci sono sempre errori di misurazione. Ci sono comunque ottime stime. Le migliori stime provengono da tre organizzazioni concorrenti, il Jet Propulsion Laboratory (i modelli di sviluppo delle effemeridi), l'Istituto russo di astronomia applicata (le effemeridi dei pianeti e della luna) e l'IMCCE (i modelli INPOP).

Nessuno di questi usa un modello kepleriano. L'eccentricità dell'orbita terrestre varia da quasi zero a 0,06 grazie alle perturbazioni di altri pianeti.

Se vuoi un buon modello approssimativo, ti suggerisco di utilizzare i valori da http: // ssd. jpl.nasa.gov/?planet_pos, che per J2000.0 ha l'orbita del baricentro Terra-Luna con un semiasse maggiore di 1,00000261 UA (149598261 km) e un'eccentricità di 0,01671123.

Gli elementi che fornisci descrivono un'orbita idealizzata che non esiste nella realtà. Questi numeri sono parametri per un modello approssimativo. La distanza più vicina dalla Terra al sole è diversa ogni anno, di molto (circa 20.000 km in effetti).

Esistono dati esatti sull'orbita terrestre?

Ci sono sicuramente modelli di gran lunga migliori di quello ellittico a 6 parametri. La soluzione migliore per un posizionamento molto accurato è una effemeride come JPL DE o VSOP. Questi modelli forniscono serie molto lunghe con letteralmente migliaia di termini, che è necessario calcolare in un dato momento per ottenere il valore di un parametro. Forniscono tali serie per un'ampia gamma di parametri orbitali in vari sistemi di coordinate e sistemi di riferimento.

In particolare, VSOP87 afferma una precisione di circa ± 4 km per la Terra - e questo è uno dei più vecchi. Un'approssimazione ellittica di base non può avvicinarsi a questo, indipendentemente dai parametri scelti. Mi capita di avere un'implementazione in giro, quindi ho eseguito alcuni numeri che coprono gli anni 2001-2010, utilizzando la serie "Variabili rettangolari baricentriche J2000". Il codice calcola X, Y e Z sia per il Sole che per la Terra e quindi trova la distanza tra loro. I numeri sono:

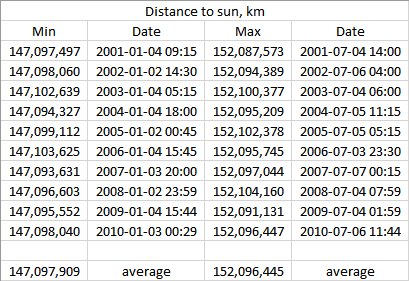
Osserva quanto sono variabili. Un'orbita perfettamente ellittica avrebbe lo stesso minimo e massimo ogni anno, ma il sistema solare è abbastanza lontano da questo.

Detto questo, la distanza media min / max concorda con I valori della NASA forniti da John Rennie e non da Wikipedia. Se desideri utilizzare il modello ellittico, questi sono i numeri migliori con cui seguire.