Suggerirei di evitare le coordinate di Schwarzschild per questo tipo di domande. Tutti gli infiniti classici (cioè il paradosso del firewall a parte) che hanno a che fare con l'orizzonte degli eventi sono dovuti a scelte di coordinate sbagliate. Desideri utilizzare un sistema di coordinate regolare all'orizzonte, come Kruskal-Szekeres. In effetti, dai un'occhiata al diagramma Kruskal-Szekeres:

(fonte: Wikipedia)

Questa è la geometria Schwarschild estesa al massimo, non un buco nero fisico che si forma da una stella crollo, ma le differenze non dovrebbero disturbarci per questa domanda. Le regioni I e III sono regioni asintoticamente piatte, II è l'interno del buco nero e IV è un buco bianco. Le iperbole in grassetto nelle regioni II e IV sono le singolarità. Le diagonali che passano per l'origine sono gli orizzonti degli eventi. L'origine (in realtà una 2-sfera con coordinate angolari soppresse) è la gola di un wormhole non attraversabile che unisce gli "universi" separati I e III. I raggi di luce radiali rimangono linee diagonali di 45 gradi sul diagramma di Kruskal-Szekeres. Le iperbole tratteggiate sono linee di coordinate $ r $ costanti di Schwarzschild, mentre i raggi radiali tratteggiati sono linee di $ t $ costanti. Puoi vedere come l'orizzonte degli eventi diventa una singolarità coordinata in cui $ r $ e $ t $ si scambiano i ruoli.

Ora se disegni una linea del mondo dalla regione I andando nella regione II diventa ovvio che attraversa l'orizzonte in un tempo proprio finito e, cosa più importante, il cono di luce passato dell'evento in cui colpisce la singolarità non può contenere l'intero spaziotempo. Quindi la risposta breve alla tua domanda è no , qualcuno che cade in un buco nero non vede la fine dell'universo. Non conosco la formula che chiedi per $ T $, ma in linea di principio puoi leggerlo dai raggi di luce sul diagramma e convertirlo in qualsiasi coordinata / tempo corretto che desideri utilizzare.

Questa è una riscrittura della risposta di Michael Brown per aiutarmi a chiarire i miei pensieri e possibilmente per aiutare tutti gli altri interessati a chiarire i loro pensieri :-) Michael presenta un molto semplice risposta alla mia domanda basata sulla geometria dello spaziotempo attorno al buco nero.

Il punto chiave è che le solite coordinate raggio / tempo di Schwarzschild sono inutili perché oscurano cosa sta succedendo. Per ovviare a questo, usiamo una trasformazione di coordinate per disegnare lo spaziotempo attorno al buco nero usando le coordinate Kruskal-Szekeres $ u $ e $ v $. Ecco come appare il risultato:

La coordinata $ u $ è orizzontale e la coordinata $ v $ è verticale.

Il problema con queste coordinate è che sono molto poco intuitive. Uno spostamento in $ u $ o $ v $ non corrisponde a nessuna quantità fisica semplice, a differenza di uno spostamento nella solita coordinata radiale $ r $ o coordinata temporale $ t $. Tuttavia le coordinate KS semplificano drasticamente le cose come segue:

In queste coordinate la costante $ r $ è un'iperbole come mostrato dalla linea tratteggiata. L'orizzonte degli eventi è la solida linea a 45 °. Puoi pensare che $ t $ aumenti man mano che sali - lo fa, anche se non in modo lineare. La singolarità è l'iperbole rossa (questo è un diagramma dello spaziotempo ricorda, quindi la singolarità è una curva non un punto). La regione che ho etichettato $ I $ è l'esterno del buco nero e la regione che ho etichettato $ II $ è la regione all'interno dell'orizzonte degli eventi. Ignora la regione del diagramma in basso a sinistra in quanto non è rilevante per la mia domanda.

Infine, la caratteristica chiave che rende possibile rispondere alla mia domanda è che tutti i raggi di luce radiali in entrata sono retti 45 ° linee che vanno dal basso a destra verso l'alto a sinistra. Ho disegnato diversi raggi di luce come le linee magenta.

Ora possiamo rispondere alla mia domanda. Iniziamo con un razzo che si libra a una distanza costante dal buco nero, che è rappresentato dall'iperbole tratteggiata nera di $ r $ costante (come ho detto sopra puoi pensare all'aumento del tempo man mano che ti sposti verso l'alto). Al momento $ t_0 $ il nostro osservatore lascia il razzo e inizia a cadere verso il buco nero. La linea blu mostra la traiettoria seguita dall'osservatore. L'osservatore colpisce la singolarità nel punto in cui le linee blu e rossa si incontrano.

Al momento $ t_1 $ il razzo emette un raggio di luce sull'osservatore in caduta. Il raggio di luce, viaggiando a 45 °, raggiunge l'osservatore prima che attraversi l'orizzonte degli eventi - finora tutto bene. Al tempo $ t_2 $ il razzo emette un secondo raggio di luce sull'osservatore, e questo raggio di luce raggiunge l'osservatore proprio mentre colpisce la singolarità. Al tempo $ t_3 $ il razzo irradia un terzo raggio di luce nel buco nero, ma questo non raggiunge l'osservatore perché l'osservatore ha già raggiunto la singolarità e non esiste più. Ciò significa che l'osservatore non vede mai il raggio di luce rilasciato al tempo $ t_3 $. L'osservatore vede alcun raggio di luce rilasciato tra $ t_0 $ e $ t_2 $, ma non vede alcun raggio di luce rilasciato dopo $ t_2 $. Quindi la linea magenta tratteggiata segna il confine tra i raggi di luce che l'osservatore può vedere e quelli che non può vedere.

Ed ecco la risposta alla mia domanda. L'osservatore non vede la fine dell'universo perché l'ultimo raggio di luce che vede è quello rilasciato alle ore $ t_2 $.

Questo non mi dà un modo semplice per calcolare il valore di $ t_2 $, perché dovrei derivare un'espressione per la traiettoria dell'osservatore in caduta (linea blu) e questo è difficile. Tuttavia, mostra che $ t_2 $ è finito quindi, usando la notazione nella mia domanda, $ T $ è limitato.

(La risposta di Michael Brown è la risposta corretta e questa è semplicemente per amplificare tramite un diagramma aggiunto.)

Di seguito è riportata la figura 31.4 da pagina 835 di Gravitazione (MTW).

Entrambi i diagrammi sono della geometria di Schwarzschild. Si noti che nelle coordinate Kruskal-Szekeres, i coni di luce appaiono come nello spaziotempo di Minkowski.

Come sottolinea Michael, le geodetiche radiali simili alla luce sono linee di 45 gradi come si può vedere guardando la geodetica B.

Chiaramente, ci sono linee del mondo simili alla luce che attraversano l'orizzonte dopo alcune linee del mondo simili al tempo in modo che la linea del mondo di un astronauta che cade radialmente verso il buco non intersechi tutto il linee del mondo radiali prima di attraversare l'orizzonte.

Inoltre, è chiaro che ci sono linee del mondo simili alla luce che terminano sulla singolarità dopo alcune linee del mondo simili al tempo.

Pertanto, l'astronauta non vede il futuro infinito prima di attraversare l'orizzonte o di incontrare la singolarità.

Inoltre, e questa è solo una nota a margine interessante da considerare, la soluzione di Schwarzschild è la statica sfericamente simmetrica em> (beh, almeno fuori dall'orizzonte) soluzione delle equazioni di Einstein. In altre parole, non esiste una "fine dell'universo" in questa soluzione .

Sono d'accordo che per uno spaziotempo che è esattamente Schwarzschild, l'osservatore in caduta non vede l'intera storia dell'universo. Tuttavia, questo risulta non essere il caso generico che ci si aspetterebbe per un buco nero astrofisico, che si è formato dal collasso di una distribuzione approssimativamente sferica della materia. Questo argomento è attualmente oggetto di ricerche attive e ci sono alcuni risultati molto interessanti su come appare effettivamente l'interno di un buco nero. Vedi, ad esempio, questo articolo recente.

La ragione per cui in Schwarzschild l'osservatore in caduta non vede l'intera storia dell'universo è che la singolarità è simile allo spazio. Ciò significa che esiste una gamma di punti in cui l'osservatore in caduta può colpire la singolarità e ogni punto può vedere solo una parte dell'universo nel suo passato causale.

Ma le persone conoscono da molto tempo altri tipi di buchi neri che non condividono questo comportamento. Gli esempi più noti sono la soluzione Reissner-Nordstrom per un buco nero carico, sfericamente simmetrico, e la soluzione Kerr per un buco nero rotante. Entrambi hanno singolarità simili al tempo e quindi la situazione è completamente diversa. Ecco un diagramma causale di un buco nero Reissner-Norstrom:

Le linee frastagliate verticali rappresentano le singolarità temporali per questo buco nero. In questo caso è possibile evitare la singolarità ed emergere in un nuovo universo che potresti attaccare in cima a questa immagine. In questo caso, quando attraversi l'orizzonte interno, dovresti essere in grado di guardare indietro e vedere l'intera storia o l'universo.

Tuttavia, questo solleva un punto problematico. L'osservatore attraversa l'orizzonte interno in un tempo proprio finito, tuttavia è in grado di vedere tutta la luce che entra nel buco nero dall'intera storia infinita dell'universo. Poiché la luce ha energia, potresti pensare che questo accumulo di radiazioni dall'universo esterno dovrebbe portare a una grande curvatura, e in effetti lo fa. Questo è noto come instabilità di inflazione di massa del buco nero. I buchi neri di Kerr condividono questa caratteristica, sebbene la struttura della singolarità in questo caso sia più complicata.

Quindi per buchi neri generici che non sono esattamente Schwarzschild, ci si aspetta un comportamento diverso. Le perturbazioni tendono a cambiare la singolarità dall'essere spaziali a comportarsi come una superficie nulla, cioè seguendo le traiettorie della luce. Un'immagine dal foglio sopra mostra questa situazione:

L'universo esterno vive nel triangolo in basso a destra di questa immagine. Le linee etichettate $ \ mathcal {CH} ^ + $ sono le singolarità nulle. Il documento ha scoperto che questa situazione era il risultato di perturbare la soluzione di Schwarzschild con materia di campo scalare. In questo caso, se cadessi nel buco nero dall'universo esterno, incapperesti nelle singolarità nulle e, supponendo di aver colpito quella a destra, vedrai tutto nell'intera storia dell'universo, nel senso che tutto ciò avrai accesso alla luce che entra nel buco nero da tempi arbitrariamente tardivi della storia dell'universo.

La risposta attualmente accettata elude la domanda sul calcolo di quali eventi possono essere effettivamente visti utilizzando le coordinate di Schwarzschild. è possibile trovare una risposta a questa domanda utilizzando le coordinate di Schwarzschild, sia numericamente che analiticamente. La risposta ovviamente è che il cono di luce passato per il caso limite non comprende l'intero universo al di fuori del buco nero e che c'è un tempo finito disponibile per segnalare a un oggetto che cade (anche nelle coordinate di Schwarzschild), che dipende da dove il l'osservatore cadente è stato rilasciato da.

Esistono due problemi separati, ciascuno con due casi separati. Il primo è capire se la luce intercetta un osservatore in caduta prima che raggiunga l'orizzonte degli eventi. Tuttavia c'è poi una piccola correzione aggiuntiva da apportare per capire se un segnale luminoso può ancora intercettare un osservatore in caduta dopo che ha attraversato l'orizzonte degli eventi ma prima di raggiungere la singolarità.

1. Se la luce può intercettare un oggetto prima che raggiunga l'orizzonte degli eventi

(a) Oggetto che cade dall'infinito

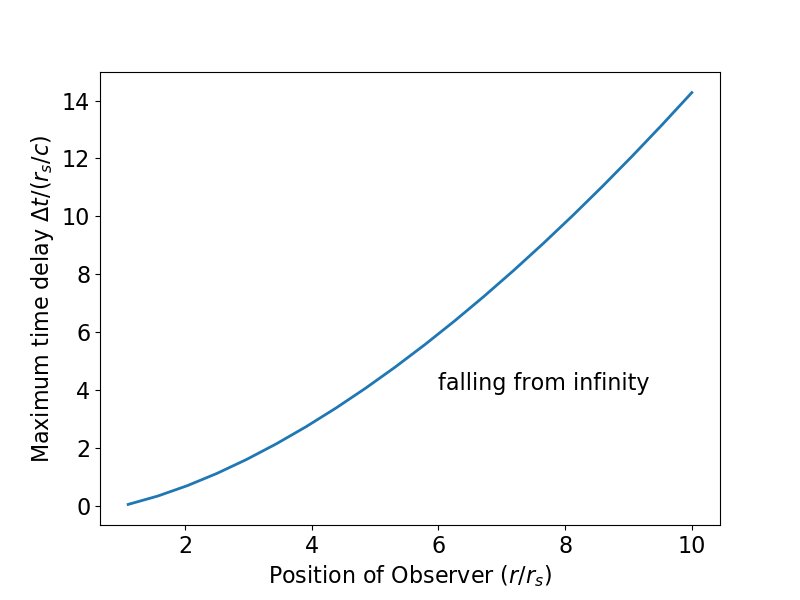
Comincio con un osservatore con un raggio $ r_0 $ (tutti i raggi sono espressi come multipli del raggio di Schwarzschild $ r_s $). L'osservatore è passato al tempo $ t_0 $ (in coordinate di Schwarzschild, che è uguale a $ \ tau = 0 $ secondo l'orologio dell'osservatore), da un oggetto che cade radialmente all'interno verso il buco nero da infinito (dove è iniziato a riposo). In un momento successivo $ \ Delta t $, l'osservatore spara un raggio laser radialmente verso l'interno. Il problema è calcolare il massimo $ \ Delta t $ che intercetterà l'oggetto in caduta e poi convertirlo in $ \ Delta \ tau $ in termini di tempo appropriato secondo l'osservatore. Che ci deve essere un massimo $ \ Delta t $ e $ \ Delta \ tau $ è concettualmente facilmente stabilito considerando (ad esempio) le coordinate Kruskal-Szekeres.

La geodetica nulla (in coordinate di Schwarzschild) seguita dalla luce che viaggia verso l'interno (in $ c = 1 $ unità) è: $$ t = -r - r_s \ ln \ left | \ frac {r -r_s} {r_0-r_s} \ right | + a + \ Delta t \,, \ tag {1} $$ dove la costante $ a = r_0 + t_0 $.

La geodetica seguita da un corpo rilasciato a riposo dall'infinito è (ad esempio, vedere l'equazione 25.38 in "Gravitation" di Misner, Thorner & Wheeler, 2017, Princeton University press) $$ t = r_s \ left (- \ frac {2} {3} \ left (\ frac {r} {r_s} \ right) ^ {3/2} - 2 \ left (\ frac {r} {r_s} \ right) ^ {1/2} + \ ln \ left | \ frac {\ sqrt {r / r_s} + 1} {\ sqrt {r / r_s} -1} \ right | \ right) + b \ tag { 2} $$ La costante $ b $ può essere scelta per garantire che l'oggetto passi per il punto $ (t_0, r_0) $ - quindi: $$ b = t_0 - r_s \ left (- \ frac {2} {3} \ left (\ frac {r_0} {r_s} \ right) ^ {3/2} - 2 \ left (\ frac {r_0} { r_s} \ right) ^ {1/2} + \ ln \ left | \ frac {\ sqrt {r_0 / r_s} + 1} {\ sqrt {r_0 / r_s} -1} \ right | \ right) \ tag { 3} $$

Tracciando queste geodetiche e utilizzando un metodo di bisezione per determinare quando e se si intersecano, sono stato in grado di determinare il massimo $ \ Delta t $ ($ T $ nell'OP, anche se ho iniziato il mio oggetto in caduta libera dall'infinito) che consente comunque alla luce di intercettare l'oggetto in caduta in funzione di dove viene emessa quella luce. Il risultato sembra stabile alla riduzione della tolleranza (ho usato $ 10 ^ {- 14} r_s $).

Un esempio del caso limite è mostrato di seguito. La curva rossa è la geodetica leggera mentre la curva blu mostra la geodetica di un oggetto che cade dall'infinito e passa attraverso (in questo caso) $ 5.8r_s $ a $ t = 0 $. Solo gli eventi al di sotto della curva rossa possono essere visti da un osservatore in caduta.

Ho quindi "derivato" questa curva in modo analitico. Riorganizzando l'equazione (1) possiamo scrivere $$ r - r_s = (r_0-r_s) \ exp ((a + \ Delta t -r) / r_s) \ exp (-t / r_s) $$ e se (vicino al limite in cui è possibile che la luce intercetti l'oggetto in caduta) lasciamo che $ t $ diventi grande, allora $ r \ rightarrow r_s $ e possiamo scrivere $$ r - r_s \ simeq (r_0 - r_s) \ exp ((a + \ Delta t -r_s) / r_s) \ exp (-t / r_s) \,, \ tag {4} $$ dove sfruttiamo il fatto che il limite di $ r \ exp (-r / r_s) $ come $ r \ rightarrow r_s $ è solo $ r / e $.

Riorganizzando l'equazione (2) in modo simile, otteniamo $$ \ frac {\ sqrt {r / r_s} - 1} {\ sqrt {r / r_s} +1} = \ exp (-t / r_s) \ exp \ left (- \ frac {2} {3} \ sinistra (\ frac {r} {r_s} \ right) ^ {3/2} -2 \ left (\ frac {r} {r_s} \ right) ^ {1/2} + \ frac {b} {r_s} \destra)\, . $$ Di nuovo, sosteniamo che attorno al caso limite $ r \ rightarrow r_s $ e quindi possiamo scrivere $$ \ sqrt {r / r_s} = 1 + 2 \ exp (b / r_s - 8/3) \ exp (-t / r_s) $$ Quadrando questo e trascurando il termine $ \ exp (-2t / r_s) $: $$ r - r_s \ simeq 4r_s \ exp (b / r_s - 8/3) \ exp (-t / r_s)) \ tag {5} $$

La presenza o meno di un punto di intercettazione dipende dal fatto che il rapporto tra le equazioni (4) e (5) sia minore di 1 per $ t \ rightarrow \ infty $. $$ \ lim_ {t \ rightarrow \ infty} \ frac {(r_0 - r_s) \ exp ((a + \ Delta t -r_s) / r_s) \ exp (-t / r_s)} {r_s (1 + 4 \ exp (b / r_s - 8/3) \ exp (-t / r_s))} < 1 \, $$ che conduce a $$ \ frac {(r_0 - r_s) \ exp ((a + \ Delta t -r_s) / r_s)} {4r_s \ exp (b / r_s - 8/3)} < 1 $$ $$ \ exp (\ Delta t / r_s) < \ frac {4r_s} {r_0 - r_s} \ exp (\ frac {b - a} {r_s} - \ frac {5} {3}) $$ $$ \ Delta t < \ ln \ left (\ frac {4r_s} {r_0 - r_s} \ right) r_s + \ left (\ frac {b - a} {r_s} - \ frac {5} {3} \ right ) r_s $$ Reinserire le espressioni per $ a $ e $ b $ $$ \ Delta t < \ ln \ left (\ frac {4r_s} {r_0 - r_s} \ right) r_s + \ left (\ frac {2} {3} \ left (\ frac {r_0} {r_s} \ right ) ^ {3/2} + 2 \ left (\ frac {r_0} {r_s} \ right) ^ {1/2} - \ ln \ left | \ frac {\ sqrt {r_0 / r_s} + 1} {\ sqrt {r_0 / r_s} -1} \ right | - \ frac {5} {3} \ right) r_s - r_0 $$ Ciò corrisponde a quanto tracciato sopra.

Per trasformare questo in un intervallo di tempo massimo corretto $ \ Delta \ tau $ dal punto di vista dell'osservatore, il risultato sarebbe moltiplicato per $ (1 - r_s / r_0) ^ {1/2} $.

(b) Oggetto che cade da fermo a $ t_0, r_0 $

Ora la configurazione è che l'osservatore rilascia l'oggetto da $ t_0, r_0 $, quindi attende un intervallo di tempo (coordinate) $ \ Delta t $ prima di segnalare.

L'equazione (1) è ancora valida in questo scenario, tuttavia l'equazione (2) deve essere sostituita dalla seguente geodetica per un oggetto che cade liberamente da fermo a $ t_0, r_0 $. $$ \ frac {t-t_0} {r_s} = \ ln \ left | \ frac {(r_0 / r_s -1) ^ {1/2} + \ tan (\ eta / 2)} {(r_0 / r_s -1) ^ {1/2} - \ tan (\ eta / 2)} \ right | + \ left (\ frac {r_0} {r_s} -1 \ right) ^ {1/2} \ left (\ eta + \ frac {r_0} {2r_s} (\ eta + \ sin \ eta) \ right). \ tag {6} $$ Qui il "parametro cicloide" $ \ eta (r) $ è definito da $$ r = \ frac {r_0} {2} (1 + \ cos \ eta) $$

Come $ r \ rightarrow r_s $, il primo termine nell'equazione (6) cresce in modo esponenziale mentre il secondo termine, che definirò $ b (r) / r_s $, tende a una costante: $$ \ lim_ {r \ rightarrow r_s} b (r) = b _ {\ rm rs} = r_s \ left (\ frac {r_0} {r_s} -1 \ right) ^ {1/2} \ left (\ eta_ {\ rm rs} + \ frac {r_0} {2r_s} (\ eta _ {\ rm rs} + \ sin \ eta _ {\ rm rs}) \ right), $$ dove $$ \ cos \ eta _ {\ rm rs} = \ left (\ frac {2r_s} {r_0} -1 \ right). $$

Usando l'identità $ \ tan \ eta / 2 = \ sin \ eta / (1 + \ cos \ eta) $, allora $$ \ tan (\ eta / 2) = \ left (\ frac {r_0} {r} - 1 \ right) ^ {1/2}. $$ Sostituendolo nell'equazione (6) possiamo impostare $ t_0 = 0 $, esponenziale e trovare $$ \ left (\ frac {r_0} {r_s} -1 \ right) ^ {1/2} \ left (1 - \ exp \ left [\ frac {bt} {r_s} \ right] \ right) = \ sinistra (\ frac {r_0} {r} -1 \ destra) ^ {1/2} \ sinistra (1 + \ exp \ sinistra [\ frac {bt} {r_s} \ destra] \ destra) $$ Quadrando questo e trascurando i termini contenenti $ \ exp (-2t / r_s) $ man mano che $ t $ diventa grande, questo può essere riorganizzato per dare $$ r = r_s \ frac {\ left (1 + 2 \ exp [(bt) / r_s] \ right)} {1 - 2 \ exp [(bt) / r_s] + (4r_s / r_0) \ exp [( bt) / r_s]}. $$ Ancora una volta, poiché stiamo cercando un comportamento limitante a $ t $ grande, il denominatore può essere espanso come un binomio, mantenendo solo i primi due termini. La moltiplicazione con il numeratore produce quindi: $$ r -r_s \ simeq 4r_s \ left (1 - \ frac {r_s} {r_0} \ right) \ exp \ left [\ frac {b-t} {r_s} \ right]. \ tag {7} $$

Per trovare il limite $ \ Delta t $ per il quale un raggio di luce dall'osservatore "catturerà" l'oggetto in caduta, prendiamo il rapporto tra le equazioni 4 e 7, impostiamo $ b = b _ {\ rm rs} $ e chiedi che sia inferiore a 1. Questo produce $$ \ exp \ left [\ frac {\ Delta t} {r_s} \ right] < 4 \ left (\ frac {r_s} {r_0} \ right) \ exp \ left [\ frac {b _ {\ rm rs} } {r_s} \ right] \ exp \ left [\ frac {r_s-r_0} {r_s} \ right] $$ e quindi $$ \ Delta t < r_s \ ln \ left (\ frac {4r_s} {r_0} \ right) + b _ {\ rm rs} + r_s - r_0 $$

Il risultato è tracciato di seguito come la curva rossa (e ho confermato che è corretto utilizzando un metodo di bisezione numerica) e confrontato al caso 1 con l'oggetto in caduta libera dall'infinito (curva blu, come nella prima immagine). Come previsto, il $ \ Delta t $ consentito è maggiore quando l'oggetto viene rilasciato da rest.

Come prima, questo risultato è l'intervallo di tempo massimo delle coordinate di Schwarzschild. Deve essere ridotto del fattore di dilatazione temporale $ (1-r_s / r_0) ^ {1/2} $ appropriato per ottenere l'intervallo di tempo appropriato massimo.

Un esempio del caso limite è mostrato di seguito. La curva rossa è la geodetica della luce, la curva blu è la geodetica dell'oggetto che cade. Solo gli eventi al di sotto della curva rossa (che asintota a un gradiente di -1) possono essere "visti" da un oggetto che cade in un buco nero da fermo, da (in questo caso) circa $ 5,8 r_s $.

2. Se la luce può intercettare un oggetto prima che raggiunga la singolarità

La risposta sopra fornisce il ritardo di tempo massimo (coordinate) affinché un segnale da un osservatore fermo raggiunga un oggetto in caduta prima che raggiunga l'orizzonte degli eventi , $ (\ Delta t) _ {\ rm EH} $. Ma questo non risponde completamente alla domanda (del titolo), perché l'oggetto può ancora ricevere luce durante il tempo necessario per raggiungere la singolarità dopo aver attraversato l'orizzonte degli eventi. Questo si vede più chiaramente nelle coordinate Kruskal-Szekeres, ma ancora una volta è possibile risolverlo (piuttosto facilmente) nelle coordinate di Schwarzschild.

La condizione qui è che il tempo delle coordinate della geodetica leggera ritardata deve essere inferiore o uguale al tempo delle coordinate della geodetica dell'oggetto in caduta a $ r = 0 $.

Questa condizione è in realtà piuttosto facile da trovare. Per il caso dell'oggetto in caduta libera dall'infinito, le equazioni (1-3) mostrano che l'originale $ \ Delta t $ che ho derivato dovrebbe essere aumentato come $$ (\ Delta t) _ {\ rm singularity} = r_s \ ln \ left (\ frac {r_s} {r_0-r_s} \ right) - r_s \ left (- \ frac {2} {3} \ left ( \ frac {r_0} {r_s} \ right) ^ {3/2} - 2 \ left (\ frac {r_0} {r_s} \ right) ^ {1/2} + \ ln \ left | \ frac {\ sqrt {r_0 / r_s} + 1} {\ sqrt {r_0 / r_s} -1} \ right | \ right) - r_0 $$ O in termini di risultato precedente. $$ (\ Delta t) _ {\ rm singularity} = (\ Delta t) _ {\ rm EH} + r_s \ left (\ frac {5} {3} - 2 \ ln 2 \ right) = (\ Delta t) _ {\ rm EH} + 0.280r_s $$

Per il caso di un oggetto che cade da fermo, vediamo che $ \ eta = \ pi $ in $ r = 0 $, in modo che se il tempo delle coordinate è inferiore o uguale al tempo delle coordinate dell'oggetto in $ r = 0 $ si ottiene dalle equazioni (1) e (6) come $$ (\ Delta t) _ {\ rm singularity} = r_s \ ln \ left (\ frac {r_s} {r_0-r_s} \ right) + \ pi r_s \ left (\ frac {r_0} {r_s} -1 \ right) ^ {1/2} \ left (1 + \ frac {r_0} {2r_s} \ right) -r_0, $$ che è maggiore di $ (\ Delta t) _ {\ rm EH} $ di un importo che dipende da $ r_0 $, ma è asintotico ai risultati della caduta dall'infinito quando $ r_0 $ diventa grande. Questa nuova relazione è tracciata di seguito: la curva rossa più alta è il ritardo massimo (tempo coordinato) che può essere tollerato e invia comunque un segnale che raggiunge l'oggetto in caduta prima della singolarità.Il grafico inferiore mostra la differenza tra questo e il risultato precedente per il ritardo per raggiungere ancora l'oggetto prima dell'orizzonte degli eventi.

La trama seguente dovrebbe rendere le cose più chiare.Mostra le geodetiche entrambi i lati o $ r_s $ nel caso di un oggetto che cade da $ r = 2r_s $ a $ t = 0 $.La geodetica chiara in rosso è quella calcolata in modo che intercetti l'oggetto come $ r \ rightarrow r_ {s} $ e ha $ (\ Delta t) _ {\ rm EH} = 3.834 r_s / c $.Ma vediamo che questa geodetica "supera" l'oggetto in caduta prima che raggiunga la singolarità a $ r = 0 $.Tuttavia, la luce verde geodetica, con $ (\ Delta t) _ {\ rm singolarità} = 4.283 r_s / c $ intercetta l'oggetto geodetica esattamente a $ r = 0 $.

Ispirato da una domanda simile, ho lavorato su questo argomento contemporaneamente a Rob Jeffries. In modo irritante, mi ha battuto; ma poiché utilizzo un approccio leggermente diverso e poiché non voglio che i miei sforzi siano vani, posterò la mia derivazione. Se non altro, serve come conferma della sua fantastica risposta :)

Cominciamo indicando le coordinate (regione I) Kruskal – Szekeres

$$ u = f (r) \ cosh \ left (\ frac {ct} {2r_ \ text {s}} \ right), \ qquad v = f (r) \ sinh \ left (\ frac {ct } {2r_ \ text {s}} \ right), \\ f (r) = \ left (\ frac {r} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \, \ text {e} ^ {r / 2r_ \ text {s }}. $$

Come è noto, in queste coordinate le geodetiche dei raggi luminosi che cadono radialmente sono linee rette ad angoli $ -45 ^ \ circ $. Infatti, se inseriamo $ u + v = k $ nelle equazioni, con $ k $ una costante, allora da $ u ^ 2 - v ^ 2 = f (r) ^ 2 $ troviamo $ k (u -v) = f (r) ^ 2 $, quindi $$ k \ exp \ left (- \ frac {ct} {2r_ \ text {s}} \ right) = f (r) = \ left (\ frac {r} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \, \ exp \ left (\ frac {r} {2r_ \ text {s}} \ right), $$ o $$ \ frac {ct} {r_ \ text {s}} = \ ln (k ^ 2) - \ frac {r} {r_ \ text {s}} - \ ln \ left (\ frac {r} {r_ \ text {s}} - 1 \ destra), $$ che sono infatti le geodetiche di un fotone in caduta radiale, con $ k = f (r_ {0, \ gamma}) $ e $ r_ {0, \ gamma} $ la posizione iniziale del fotone a $ t = 0 $.

Ora, supponiamo di avere un oggetto in caduta radiale, che inizia a riposo in una posizione $ r_0 $ a $ t = 0 $. Quali fotoni in caduta radiale raggiungeranno l'oggetto prima che attraversi l'orizzonte degli eventi? Per rispondere a questa domanda, proveremo a derivare la geodetica di un fotone in caduta radiale in modo tale da raggiungere l'oggetto proprio all'orizzonte degli eventi.

La geodetica di un oggetto in caduta radiale può essere scritta nella forma (Misner, Thorne & Wheeler Eq. (31.10), Pag. 824) $$ \ begin {align} r & = \ frac {r_0} {2} (1+ \ cos \ eta) = r_0 \ cos ^ 2 \ eta / 2, \\ \ frac {c \ tau} {r_ \ text {s}} & = \ frac {1} {2} \ left (\ frac {r_0} {r_ \ text {s}} \ right) ^ {\! 3 / 2} (\ eta + \ sin \ eta), \\ \ frac {ct} {r_ \ text {s}} & = \ ln \ left (\ frac {\ sqrt {r_0 / r_ \ text {s} -1} + \ tan \ eta / 2} {\ sqrt {r_0 / r_ \ text {s} -1} - \ tan \ eta / 2} \ right) + \ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2 } \ left (\ eta + \ frac {r_0} {2r_ \ text {s}} (\ eta + \ sin \ eta) \ right). \ end {align} $$ È anche istruttivo introdurre l'energia totale (adimensionale) dell'oggetto $$ E = \ frac {\ mathcal {E}} {mc ^ 2} = \ left (1- \ frac {r_ \ text {s}} {r} \ right) \ frac {\ text {d} t} {\ testo {d} \ tau}. $$ Le orbite radiali soddisfano l'equazione $$ \ left (\ frac {\ text {d} r} {c \, \ text {d} \ tau} \ right) ^ 2 = E ^ 2 - \ left (1- \ frac {r_ \ text {s}} {r} \ right), $$ quindi se l'oggetto è a riposo nella posizione $ r_0 $ in $ t = \ tau = 0 $, allora $$ E = \ sqrt {1- \ frac {r_ \ text {s}} {r_0}}. $$ L'equazione per $ t (\ eta) $ può quindi essere riscritta come $$ \ frac {ct} {r_ \ text {s}} = \ ln \ left (\ frac {E + \ sqrt {1-E ^ 2} \ tan \ eta / 2} {E - \ sqrt {1-E ^ 2} \ tan \ eta / 2} \ right) + \ frac {E} {\ sqrt {1-E ^ 2}} \ left (\ eta + \ frac {\ eta + \ sin \ eta} {2 (1 -E ^ 2)} \ right). $$ Successivamente, seguirò questo articolo (che contiene alcuni errori) per ricavare come si comporta questa equazione quando $ r $ si avvicina all'orizzonte degli eventi. Scriviamo $$ r = r_ \ text {s} (1+ \ varepsilon), \ qquad \ varepsilon \ rightarrow 0. $$ Vicino all'orizzonte degli eventi possiamo ignorare i termini di ordine superiore in $ \ varepsilon $, quindi $$ \ begin {align} \ cos ^ 2 \ eta / 2 & = (1+ \ varepsilon) \ frac {r_ \ text {s}} {r_0} = (1+ \ varepsilon) (1-E ^ 2) = 1 - E ^ 2 + \ varepsilon (1-E ^ 2), \\ \ sin ^ 2 \ eta / 2 & = E ^ 2 - \ varepsilon (1-E ^ 2), \ end {align} $$ e $$ \ begin {align} (1-E ^ 2) \ tan ^ 2 \ eta / 2 & = \ frac {E ^ 2 - \ varepsilon (1-E ^ 2)} {(1+ \ varepsilon)} \\ & \ approx \ sinistra [ E ^ 2 - \ varepsilon (1-E ^ 2) \ right] (1- \ varepsilon) \\ & \ approx E ^ 2 - \ varepsilon (1-E ^ 2) - \ varepsilon) E ^ 2 = E ^ 2 - \ varepsilon. \ end {align} $$ Perciò, $$ \ begin {align} E + \ sqrt {1-E ^ 2} \ tan \ eta / 2& \ approx E \ sinistra (1 + \ sqrt {1 - \ varepsilon / E ^ 2} \ destra) \\ & \ approx 2E - \ frac {\ varepsilon} {2E} \ approx 2E, \ end {align} $$ e $$ \ begin {align} E - \ sqrt {1-E ^ 2} \ tan \ eta / 2& \ approx E \ left (1 - \ sqrt {1 - \ varepsilon / E ^ 2} \ right) \\ & \ approx \ frac {\ varepsilon} {2E}, \ end {align} $$ In modo che finalmente, come $ r \ rightarrow r_ \ text {s} $, $$ \ frac {ct_ \ text {s}} {r_ \ text {s}} \ approx \ ln \ left (\ frac {4E ^ 2} {\ varepsilon} \ right) + \ frac {E} {\ sqrt {1 -E ^ 2}} \ sinistra (\ eta_ \ text {s} + \ frac {\ eta_ \ text {s} + \ sin \ eta_ \ text {s}} {2 (1-E ^ 2)} \ destra ), $$ con $ \ eta_ \ text {s} $ il valore di $ \ eta $ all'orizzonte degli eventi. Da $ \ cosh (x) = \ sinh (x) \ rightarrow \ text {e} ^ x / 2 $ as $ x \ rightarrow \ infty $, le coordinate Kruskal – Szekeres dell'oggetto all'orizzonte degli eventi diventano (da $ t \ rightarrow \ infty $) $$ \ begin {align} u_ \ text {s} ^ 2 = v_ \ text {s} ^ 2 & = \ frac {1} {4} f (r_ \ text {s}) ^ 2 \, \ exp \ left (\ frac {ct_ \ text {s}} {r_ \ text {s}} \ right) = \ frac {\ varepsilon \ text {e}} {4} \ exp \ left (\ frac {ct_ \ text {s}} {r_ \ text {s}} \ right) \\ & = \ text {e} E ^ 2 \ exp \ left [\ frac {E} {\ sqrt {1-E ^ 2}} \ left (\ eta_ \ text {s} + \ frac {\ eta_ \ text {s} + \ sin \ eta_ \ text { s}} {2 (1-E ^ 2)} \ right) \ right], \ end {align} $$ o $$ \ begin {align} u_ \ text {s} = v_ \ text {s} & = \ sqrt {\ text {e}} E \ exp \ left [\ frac {E} {2 \ sqrt {1-E ^ 2}} \ left (\ eta_ \ text {s} + \ frac {\ eta_ \ text {s} + \ sin \ eta_ \ text {s}} {2 (1-E ^ 2)} \ right) \ right] \\ & = \ sqrt {\ text {e}} \ sqrt {\ frac {r_ \ text {s}} {r_0}} \ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \ exp \ left [\ frac {1} {2} \ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \ left (\ eta_ \ text { s} + \ frac {r_0} {2r_ \ text {s}} (\ eta_ \ text {s} + \ sin \ eta_ \ text {s}) \ right) \ right]. \ end {align} $$ Le coordinate corrispondenti per un fotone in caduta radiale soddisfano $ u_ \ text {s} + v_ \ text {s} = k_ \ text {b} $, per qualche valore limite $ k_ \ text {b} $. Quindi $ k_ \ text {b} = 2u_ \ text {s} $ e troviamo la corrispondente geodetica nulla $$ \ frac {ct} {r_ \ text {s}} = \ ln (k_ \ text {b} ^ 2) - \ frac {r} {r_ \ text {s}} - \ ln \ left (\ frac {r } {r_ \ text {s}} - 1 \ destra). $$ Potremmo risolverlo per $ r $ a $ t = 0 $, che produce un raggio di confine $ r_ \ text {b} $ oltre il quale i fotoni in caduta radiale non possono raggiungere l'oggetto prima che attraversi l'orizzonte degli eventi. In alternativa, potremmo inserire $ r = r_0 $ e chiedere qual è il tempo massimo $ \ Delta t $ tale che i fotoni inviati a $ r_0 $ prima di $ t = \ Delta t $ possano ancora raggiungere l'oggetto. Noi troviamo $$ \ begin {align} \ frac {c \ Delta t} {r_ \ text {s}} & = \ ln (k_ \ text {b} ^ 2) - \ frac {r_0} {r_ \ text {s}} - \ ln \ left ( \ frac {r_0} {r_ \ text {s}} - 1 \ destra) \\ & = 1 + \ ln \ left (\ frac {4r_ \ text {s}} {r_0} \ right) + \ left [\ left (\ frac {r_0} {r_ \ text {s}} - 1 \ right) ^ {\! 1/2} \ left (\ eta_ \ text {s} + \ frac {r_0} {2r_ \ text {s}} (\ eta_ \ text {s} + \ sin \ eta_ \ text {s} ) \ right) \ right] - \ frac {r_0} {r_ \ text {s}}, \ end {align} $$ che è esattamente lo stesso risultato fornito da Rob Jeffries.

Ho creato una trama per visualizzare i risultati, nelle coordinate di Schwarzschild e Kruskal – Szekeres:

La curva blu è la geodetica di un oggetto, a riposo a $ t = 0 $ (qui, $ r_0 = 2r_ \ text {s} $). La curva arancione è la geodetica di un fotone che si trova nella posizione $ r_0 $ in $ t = 0 $. La curva rossa è la geodetica che ho derivato in questo post. Inizia dalla posizione $ r_ \ text {b} $ a $ t = 0 $ e raggiunge l'oggetto proprio all'orizzonte degli eventi. Le geodetiche dei fotoni che si trovano tra le curve arancione e rossa (ne ho tracciate due, le curve tratteggiate) raggiungeranno l'oggetto, le geodetiche oltre la curva rossa no.

Per aggiungere alle eccellenti risposte sopra, ecco un diagramma dello spaziotempo in coordinate Gullstrand-Painleve o "pioggia".Questo è tratto dal superbo e accessibile libro Exploring Black Holes (2000) di Taylor & Wheeler, $ \ S B.6 $.La loro metafora "pioggia" significa una particella di prova con massa, che inizialmente cadde dal riposo lontano dal buco nero.Considerali come astronauti / osservatori, per questo problema.

$ t_ \ textrm {rain} $ è il tempo corretto di una goccia di pioggia, che è usata come coordinata.$ r $ è la solita coordinata di curvatura come nelle coordinate di Schwarzschild [-Droste] e $ M $ è la massa del buco nero.Il diagramma mostra che la maggior parte degli "impulsi luminosi" non raggiunge mai un dato "stantuffo pioggia";in particolare non vedranno la fine dell'universo.

No. Il buco nero evaporerà completamente in un tempo finito, quindi entro la fine dell'universo non esisterà più.

La tua domanda è dovuta a una certa confusione con il concetto di spaziotempo di un buco nero. Devi distinguere tra il tuo sistema di coordinate e ciò che vedi. Entrambi sono concetti diversi: Un semplice esempio è uno spazio di Minkowski: se un diagramma di Minkowski rappresenta le tue coordinate, ottieni una visione quadridimensionale dell'intero spaziotempo. Al contrario, ciò che vedi sono elementi che si trovano sul tuo cono luminoso che mostra il passato.

Vicino a un buco nero dobbiamo applicare la stessa distinzione di questo duplice concetto che può essere mostrato nel seguente diagramma di Kruskal, con una particella in caduta A e una particella che rimane fuori B:

Le coordinate temporali di un osservatore lontano sono indicate dalle linee che passano per il centro: t = 0, t = 1, t = 2, limitate dall'orizzonte degli eventi dove t = $ \ infty $. Secondo queste coordinate temporali, la particella in caduta non raggiungerà mai l'orizzonte. E viceversa, quando A si avvicina all'orizzonte, l'orologio di un osservatore esterno si avvicinerà alla fine del tempo.

Forse questo è il motivo per cui hai posto la tua domanda. Ma la tua domanda non è chiedersi: qual è la posizione rispetto alle coordinate di un osservatore esterno, ma: cosa vede la particella in caduta, e per questa domanda devi fare riferimento (come mostrato in altre risposte) al piccolo 45 ° - frecce tra le particelle comunicanti A e B. Le 3 frecce diagonali dal basso verso sinistra mostrano che B si trova a un certo punto quando A tocca l'orizzonte degli eventi.