Sì, i logaritmi danno sempre numeri adimensionali, ma no, non è fisico prendere il logaritmo di qualsiasi cosa con unità.

Invece, c'è sempre qualche unità standard. Per il tuo esempio, lo standard è il chilometro. Quindi 20 km, sotto la trasformazione del log, diventa $ \ ln (20 \; \ textrm {km} \; / \; \ textrm {km} \;) $. Allo stesso modo, il logaritmo di 10 cm, con questa scala, è
$$ \ ln (10 \; \ textrm {cm} \; / 10 \; \ textrm {km} \;) = \ ln (10 \ times 10 ^ {- 3} / 10 ^ {3}) = \ ln (10 ^ {- 5}) $$

Ecco una risposta "matematica" ma altamente non fisica .

Usando quella $ km \ cdot km = (km) ^ 2 $ ecc, possiamo definire formalmente l'aritmetica dei numeri con unità su un ' algebra graduata $ A = \ oplus_ {k \ in \ mathbb {N}} V_k $ dove $ V_k = \ otimes ^ k V $ dove $ V $ è trattato come uno- spazio vettoriale reale dimensionale ($ V_0 $ è lo scalare $ \ mathbb {R} $). La scelta dell'unità è la scelta di un vettore base in $ V $. $ V_0 $ sono gli scalari puri. Quindi, per ogni scelta di un vettore base $ v \ in V $, otteniamo la mappatura dalla sequenza infinita $ \ mathbb {R} ^ {\ mathbb {N}} \ ad A $ realizzando quella sequenza tramite $ (r_k) \ a [r_k] _v = \ sum r_k (\ otimes ^ kv) $. Definiamo la moltiplicazione $ V_k \ volte V_ {k '} \ a V_ {k + k'} $ come al solito.

(Per ora non definiremo le unità di potenza negative. Ma probabilmente possono essere incorporate in modo analogo.)

Quindi formalmente possiamo definire $ \ exp: A \ to A $ dall'espansione della serie di potenze

$$ \ exp a = \ sum_ {k = 0} ^ {\ infty} \ frac {1} {k!} a ^ k $$

dove $ a ^ k $ è definito nel senso dell'algebra graduata. E lì, abbiamo definito cosa significa $ \ exp $ di qualcosa con unità. Il cambio di base di $ \ exp $ è gestito da $ y ^ a = \ exp (\ ln (y) \ cdot a) $. Allo stesso modo il cambio di unità è naturalmente incorporato, sfruttando il fatto che un cambiamento di base su uno spazio vettoriale reale unidimensionale è solo una moltiplicazione per scalari. In altre parole, abbiamo $ [r_k] _v = [r'_k] _ {v '} $ dove $ r_k = s ^ kr'_k $ quando $ v = s v' $.

Usando questo possiamo invertire formalmente l'espansione della serie di potenze per trovare cosa dovrebbe essere $ \ ln $ ". Correggi un'unità $ v $. Prendi $ (r_k) \ in \ mathbb {R} ^ {\ mathbb {N}} $ e considera $ [r_k] _v \ in A $. Per trovare $ \ ln [r_k] _v $ dobbiamo trovare $ (s_k) \ in \ mathbb {R} ^ {\ mathbb {N}} $ in modo tale che

$$ \ begin {align} r_0 & = \ exp s_0 \\ r_1 & = e ^ {s_0} s_1 \\ r_2 & = e ^ {s_0} (s_2 + \ frac {1} {2} s_1 ^ 2) \\ & \ vdots \ end { align} $$

(Possiamo anche usare l'espansione di Taylor di $ \ ln $ intorno a $ 1 \ in \ mathbb {R} $ per ottenere l'espressione per $ (s_k) $ in termini di $ (r_k) $.)

Purtroppo anche in questo frame il lavoro $ \ ln 1 km $ non è ancora ben definito: nell'immagine di $ \ exp $, $ r_0 $ è necessariamente positivo. Formalmente, è possibile definire $ \ ln (1 km) = \ ln (1 + (1 km - 1)) $ come la serie di potenze piuttosto divergente

$$ \ ln (1 m) = \ sum \ frac {(- 1) ^ {k + 1}} {k} (-1 + 1 (m)) ^ k = \ sum \ frac {-1} {k} + \ sum 1 (m) - \ sum \ frac {k-1} {2} (m ^ 2) + \ cdots $$

Ora un po 'di divertimento con le serie divergenti: nota che $ \ sum 1 = \ sum (-1) ^ k (-1) ^ k = \ sum (-1) ^ kx ^ k | _ {- 1} $ è l'espansione in serie di Taylor di $ 1 / x $ intorno a $ x_0 = 1 $ valutata a $ -1 $, quindi il secondo termine è nominalmente $ \ lim_ {x \ to 0+} 1 / x $. Quindi, anche se regolarizziamo:

$$ \ lim _ {\ delta \ to 0+} \ ln (\ delta + 1m) = \ lim _ {\ delta \ to 0+} \ ln \ delta + \ delta ^ {- 1} m + \ cdots $$

è ancora fortemente divergente.

(Si noti, tuttavia, che $ \ ln (1 + 1km) = \ sum (-1) ^ {j + 1} / j (km) ^ j $ è ben definito come una potenza formale serie.)

Allora qual era lo scopo di questo post? Questo post è principalmente indirizzato alla conclusione che $ \ log m $ è un "numero adimensionale" come affermato nella dichiarazione della domanda. Mentre nella solita aritmetica ci viene insegnato che non possiamo aggiungere mele alle arance, questo è solo se prendiamo il punto di vista di provare ad aggiungere un oggetto nel $ \ mathbb {Z} $ - modulo di mele a un oggetto separato in il $ \ mathbb {Z} $ - modulo delle arance. Se sei disposto a lavorare nel modulo a somma diretta di mele $ \ oplus $ arance, puoi effettivamente aggiungere mele alle arance.

Ora, implicitamente nell'affermare che $ \ log $ ha senso per oggetti con unità, (e analogamente che $ \ exp $ ha senso per oggetti di unità), è necessario che lavoriamo già in un sistema, quello del graded $ \ mathbb {R} $ - algebra, in cui puoi aggiungere uno scalare (un oggetto senza unità) a un vettore (un oggetto con unità). Quindi, nell'affermare che si vuole dare un senso a $ \ log km $, non si può concludere da esso che $ 3 $ e $ \ log m $ debbano avere le stesse unità.

Questa è una domanda divertente. Ho difficoltà a capire bene la trasformazione che è $ ln $, quindi scriverò le cose in termini di esponenti.

$$ \ mathrm {value} = \ ln (10 \ \ mathrm {km}) $$$$ e ^ {\ mathrm {value}} = 10 \ \ mathrm {km} $$

Il numero $ e $ è, ovviamente, senza unità. Se elevo un numero a una potenza, quali sono le unità di potenza consentite? Se scrivo $ x ^ 2 $, ho un presupposto intuitivo che $ 2 $ non ha unità, perché è solo un conteggio usato per esprimere $ x \ times x = x ^ 2 $.

Quindi, Mi sono convinto della risposta di Carl e richiederei un logaritmo per avere un riferimento per avere un senso. Ad esempio:

$$ e ^ {\ mathrm {value}} = \ frac {10 \ \ mathrm {km}} {1 \ \ mathrm {km}} $$

La precedente alternativa di $ e $ elevata a una potenza pari a una quantità fisica con unità reali sembra l'esempio perfetto di qualcosa che non ha senso.

log plots

Ho un'altra domanda che nasce dalla tua domanda e cercherò di rispondere qui. Ricordo in particolare di aver preso la derivata dei grafici log-log e linear-log nelle classi di ingegneria. Avevamo qualche giustificazione per questo, ma in superficie sembrerebbe priva di senso, quindi tuffiamoci. Ecco un esempio di un diagramma di registro. Mostrerò il grafico e poi offrirò un'equazione della linea che viene rappresentata.

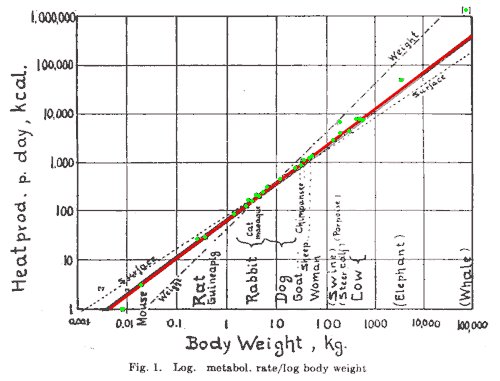
^{Fonte immagine: Wikipedia}

Inizierò a scrivere cose dal modulo $ y = mx + b $ di base, quindi cambierò le cose se necessario. Dato che sto usando una costante arbitraria, la elencherò ogni volta che sarà necessario.

$$ \ log (p) = a \ log (m) + b = a (\ log (m) + b ') = a \ log (b' 'm) = \ log (b' '^ am ^ a) = \ log \ bigg (\ frac {p_0} {m_0 ^ a} m ^ a \ bigg) $$$$ p = p_0 \ left (\ frac {m} {m_0} \ right) ^ a $$

Come per magia, emerge una forma riconoscibile. Osservare una relazione lineare in un grafico log-log significa davvero che stai osservando un adattamento di potenza, non un adattamento lineare. Uno studente può ancora chiedere "ma cosa sono aeb", il che è un po 'più difficile. In primo luogo, non ho manipolato $ a $, quindi puoi prendere il significato direttamente dalla forma finale, vale a dire che è un esponente e quindi senza unità. Per b:

$$ b = ab '= a \ log (b' ') = a \ log \ bigg (\ frac {p_0 ^ {1 / a}} {m_0} \ bigg) = \ log \ left (\ frac {p_0} {m_0 ^ a} \ right) $$

Questo mostra che $ b $ è anche senza unità, ma fornisce anche interpretazione a $ p_0 $, che è il valore y di riferimento in corrispondenza di un valore x di riferimento ($ m_0 $). Passerò al grafico a log lineare o a una scala semi-logaritmica.

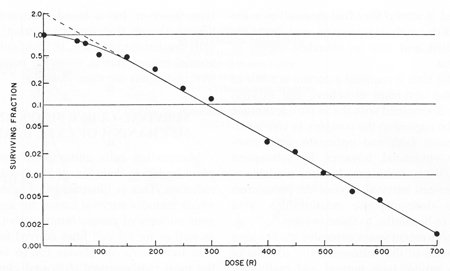
^{Fonte immagine: J. Exp. Med. 103 , 653 (1956).}

Denoterò $ f $ per "frazione sopravvissuta" e $ d $ per dose. L'equazione per una regressione che appare lineare nel grafico precedente sarà la seguente.

$$ \ log (f) = ad + b $$$$ f = e ^ {ad + b} = e ^ be ^ {ad} = f_0 e ^ {ad} $$

È importante notare qui che $ b $ ha sempre avuto unità dubbie, proprio come nel caso log-log, ma non " Non importa perché una forma più utile esce naturalmente dalla matematica. Il valore $ f_0 $ sarebbe il valore di base (100% in questo caso) a $ d = 0 $.

Riepilogo: ipotizzando una relazione lineare nei grafici logaritmici, si presume che la relazione effettiva segua alcuni non lineare e le unità funzioneranno una volta che avrai fatto i calcoli matematici, ma l'interpretazione dei valori potrebbe non essere banale.

È qualcosa che non è né una quantità fisica né un numero adimensionale, ma qualcosa che può essere semplicemente descritto come logaritmo di una quantità fisica . Non ci sono molti problemi con questo: sia $ \ mathcal {P} $ lo spazio delle quantità fisiche. Possiamo estendere questo spazio in modo simile allo spazio vettoriale per unità fisiche di base (es. SI) come descritto da Willie Wong. Ciò che è importante: sappiamo che non possiamo eseguire determinate operazioni in questo spazio, ad esempio non possiamo aggiungere una massa a una corrente elettrica. L'addizione di quantità $ a, b \ in \ mathcal {P} $ è definita solo se $ a $ e $ b $ hanno la stessa dimensione, cioè se $ \ esiste x \ in \ mathbb {R} $ tale che $ a = xb $. La moltiplicazione è sempre definita e restituisce sempre una quantità fisica. (Questo definisce anche le potenze delle quantità fisiche, ma non quello che, diciamo, l'esponenziale di una di esse è.)
Sappiamo quindi che $ \ mathbb {R} \ subset \ mathcal {P} $, poiché per, diciamo , due lunghezze $ a, b \ in \ mathcal {P} $ il rapporto $ \ tfrac {a} b $ sarà un numero adimensionale. Per queste quantità adimensionali, il logaritmo è definito dall'inizio.

È abbastanza semplice estenderlo a uno spazio pieno $ \ ln \! \! \ Mathcal {P} \ supset \ mathbb {R} $: per $ a \ in \ mathbb {R} \ subset \ mathcal {P} $, il logaritmo è definito come di consueto. Per $ a \ not \ in \ mathbb {R} $, definiamo il logaritmo assiomaticamente: prima richiediamo che $ \ ln \! \! \ Mathcal {P} $ sia un'addizione WRT di un gruppo abeliano, anche uno spazio vettoriale superiore a $ \ mathbb {R} $. Quindi, per $ \ lambda \ in \ mathbb {R} $, $$ \ begin {align} \ ln (a ^ \ lambda) &: = \ lambda \ ln (a) \ end {align} $$ e per $ b \ in \ mathcal {P} $, $$ \ ln (ba): = \ ln (b) + \ ln (a). $$ A condizione che $ a $ e $ b $ abbiano la stessa dimensione e quindi possano essere aggiunti, questo già ci dice il logaritmo della somma: sappiamo che allora $ \ esiste x \ in \ mathbb {R} \ due punti b = ax $ , in altre parole possiamo scrivere qualsiasi somma di quantità fisiche come prodotto di una di esse con un numero reale, quindi il logaritmo di qualsiasi lunghezza si riduce al logaritmo di una determinata lunghezza, più il logaritmo del rapporto tra le lunghezze .

Tornando alla tua domanda: qual è il logaritmo di un chilometro? La risposta: $ \ ln (1 \: \ mathrm {km}) = \ ln (\ mathrm {km}) $. Se tratti i chilometri come unità di base della lunghezza, questo è tutto ciò di cui hai bisogno. Se preferisci metri o pollici o qualsiasi altra cosa, ottieni $$ \ ln (1 \: \ mathrm {km}) = \ ln (1000 \: \ mathrm {m}) = \ ln (1000) + \ ln (\ mathrm {m}) $$$$ \ ln (1 \: \ mathrm {km}) = \ ln (\ tfrac {1 \: \ mathrm {km}} {1 "} \: \ mathrm {"}) = \ ln (\ tfrac {1 \: \ mathrm {km}} {1 "}) + \ ln (\ mathrm {"}) \ approx 10.58 + \ ln (\ mathrm {"}) $$ Qui, $ \ ln (\ mathrm {km}), \ ln (\ mathrm {m}), \ ln (\ mathrm {"}) $ sono non numeri adimensionali. Pensali piuttosto come elementi di uno spazio vettoriale che ha i numeri reali come sottospazio.

Il modo migliore per pensarci è che un numero come 1 km è costituito da 1 adimensionale moltiplicato per un'unità, km. Quando prendi il log di un prodotto, ottieni la somma dei log, quindi log (1 km) è uguale a log (1) + log (km). Ciò mostra che il log di 1 km non è né una quantità adimensionale né una quantità adimensionale. Se fosse adimensionale, sarebbe esprimibile senza riferimento a nessun sistema di unità. Se fosse dimensionato, cambierebbe per moltiplicazione quando il sistema di unità veniva modificato. Non è nessuna di queste cose.

La cosa più simile alle "unità logaritmiche" sono i decibel, che sono 10 volte il logaritmo in base 10 di un rapporto. Per inserire una quantità fisica in un'unità simile a un decibel, è necessario prima dividere per una quantità di riferimento. Ad esempio, l'unità "decibel" per la potenza è "dBm", che è il rapporto tra la potenza in questione su 1 mW, espresso in dB:

$ $ P _ {\ rm dBm} = 10 \ {\ rm log_ {10}} \ left (\ frac {P _ {\ rm mW}} {1 \ \ rm mW} \ right) $$

La funzione logaritmica viene facilmente utilizzata per la trasformazione da una scala all'altra. Infatti una scala / unità è una misura e quindi senza dimensioni, ma per interpretare in senso fisico ci appropriamo di un'unità relativa a uno standard assoluto affinché il valore abbia senso e sia riproducibile. Rispondendo così alla tua domanda. Log (x) è senza unità, poiché tutte le operazioni matematiche eseguite sono intrinsecamente senza unità .. Per una migliore comprensione vorrei fare un esempio immaginario: "Quando vado a correre con il mio amico la distanza tra noi è proporzionale alla velocità di corsa del mio amico in "In questo esempio le unità su entrambi i lati dell'uguaglianza sono completamente arbitrarie a seconda della formulazione della situazione, potrebbe essere senza dimensioni - m / so diciamo tempo e poi celsius - m / s!

Spero che questo aiuti.

Per una visione alternativa della potenziale "assenza di dimensione" della funzione logaritmo, correlata alla sua relazione con gli integrali e le derivate delle funzioni di potenza, e la sua vicinanza alla funzione $ 0 $ -esima potenza. Se si calcola una primitiva di $ t ^ p $: $$ \ int t ^ p dt \ ,, $$ con $ p \ neq -1 $, si ottiene, a intervalli ben definiti:
$$ \ frac {1} {p +1} \ times t ^ {p + 1} \,. $$

Ogni volta, si guadagna un'altra dimensione (o un potere per la rispettiva unità). Quando si differenzia, si perdono dimensioni fino a grado $ 0 $ per poteri positivi. Per potenze negative, questo scende a $ - \ infty $: for $ p \ neq 0 $,

$$ \ frac {d (t ^ p)} {dt} = pt ^ {p- 1} $$

Sicuramente sta succedendo qualcosa intorno alla potenza zero.

È consuetudine impostare una potenza zero di uno scalare $ \ alpha $ non nullo su $ 1 $ ($ \ alpha ^ 0 = 1 $). Se ora aggiusti un $ t $ non nullo, il coefficiente di variazione per una potenza $ p $ reale vicino a $ 0 $ sarà simile a: $$ \ frac {e ^ {p \ log t} - t ^ 0} {p -0} \ approx \ frac {1 + p \ log t - 1} {p} $$ poiché $ p $ tende a $ 0 $. Da qui il comportamento $ \ log t $ .

In un certo senso, una costante è un comportamento limite del logaritmo, o viceversa. Quindi, il logaritmo dovrebbe essere in qualche modo senza unità.

Ci sono concetti simili nell'analisi statistica dei dati sperimentali. Quando si tenta di trovare una relazione tra le variabili $ y $ e $ t $ e non si riesce a trovarne una lineare, alcuni tentano di modificare almeno una variabile con una funzione di potenza. J. Tukey ("inventore" del box-plot e della FFT) ha proposto la scala di trasformazione, o scala dei poteri, guardando $ y = a + bt ^ {p} $. Una soluzione più soddisfacente sta nella trasformata di Box-Cox: se $ \ hat {t} $ denota la media geometrica di $ t $ e $ \ alpha $ qualche spostamento, allora: $$ t_ \ alpha ^ {(p)} = \ frac {(t- \ alpha) ^ p - 1} {p \ hat {t} ^ {p-1}} $$ dove vedi che si fa molta attenzione a mantenere la stessa "unità" tra $ t_ \ alpha ^ {(p)} $ e $ t $. Indovina un po? Per $ p = 0 $, impostano $ t_ \ alpha ^ {(0)} = \ hat {t} \ log (t + \ alpha) $.

In una parola, la $ 0 $ -esima potenza di una costante è $ 1 $, la $ 0 $ -esima potenza di una variabile è la sua $ \ log $. Somewhow.

Riferimenti:

• J. W. Tukey, Analisi esplorativa dei dati. Addison-Wesley, 1977.
• G. E. P. Box e D. R. Cox, An analysis of transformations, Journal of the Royal Statistical Society. Serie B, 1964.
• Correlato a Stackexchange: Successore moderno di Exploratory Data Analysis di Tukey?

In primo luogo, la domanda è un po 'mal posta. In un grafico di registro, ad esempio, le quantità sono (log X) km , non log (X km) . Dobbiamo definire ulteriormente la domanda: cosa significa "prendere un logaritmo"? Il logaritmo, o qualsiasi funzione simile, è definito per prendere un numero reale o complesso e dare un nuovo numero basato su una certa regola. Dare qualcosa di diverso da un numero è un po 'come chiedere "Quanto pesa il numero tre?"; non ha senso perché la funzione che dà il peso di un oggetto non accetta numeri.

(Considera le equazioni fisiche che coinvolgono quantità fisiche come argomenti di logaritmi, funzioni trigonometriche o come esponenti. L'esperienza ci dice che, nelle equazioni derivanti dalla natura, le unità di quantità all'interno di esponenti e funzioni si combinano sempre per dare un numero adimensionale. Qualsiasi espressione significativa deve provenire dal ragionamento fisico, quindi dovresti arrivare a questa domanda anche dal ragionamento fisico ..)

Come ha notato Ben Cromwell nel suo commento, sono sicuro che ci sono modi per rappresentare le unità in matematica.

I miei due centesimi sono che questo è un classico mix di meta livelli.

Un chilometro è una misura sul terreno della terra. Quando creiamo una mappa, un meta livello per la misura effettiva, la lunghezza sulla mappa è forse 1 cm ogni dieci chilometri, e lo prendiamo a nostro agio senza chiederci come sia possibile. È possibile perché abbiamo molto chiaramente il concetto della mappa come un meta livello.

Supponiamo di creare la mappa su scala logaritmica (esistono mappe divertenti del globo a seconda delle funzioni). Ciò significherebbe che ciò che sarebbe contrassegnato come un chilometro su questa mappa diventerà logaritmicamente più grande man mano che i dati reali (non meta) aumentano in chilometri. Il motivo per cui si usano i meta livelli per quantità che hanno unità è per comodità, proiettare il globo su un aereo è conveniente per quello che vogliamo fare, sebbene distorca la dimensione relativa del chilometro sulla mappa, che la nostra "intuizione" vuole costante .

Quando abbiamo a che fare con esponenti e logaritmi nelle equazioni fisiche, siamo molto attenti ad avere numeri adimensionali. In realtà è uno degli strumenti che bilancia le unità. Studia la distribuzione Boltzmann come esempio.

In qualche modo le unità di fisica continuano a confondere le persone. Un modo semplice per uscire da questa confusione è rendersi conto che tradurre la fisica in matematica richiede di trasformare il problema in uno che si occupi solo di numeri puri (cosiddetti adimensionali).

Questo può essere semplice. Considera un semplice pendolo. Determinare il periodo di tempo per oscillare il bob $ t_ {swing} $ richiede di lanciare il problema in forma matematica. Questo ci costringe a lavorare non con il periodo di tempo stesso, ma con una quantità adimensionale come il rapporto tra $ t_ {swing} $ e qualche altro tempo $ t_0 $. Di conseguenza possiamo derivare equazioni come $$ \ frac {t_ {swing}} {t_0} \ = \ f (..) $$ In caso di pendolo, il problema contiene un parametro temporale sotto forma di radice quadrata della sua lunghezza diviso per l'accelerazione gravitazionale locale: $ t_0 = \ sqrt {l / g} $. Quindi si tenta di trovare un'espressione della forma

$$ \ frac {t_ {swing}} {\ sqrt {l / g}} \ = \ f (..) $$

Quando si esegue l'analisi per piccoli angoli di oscillazione, ne consegue che $ f (..) = 2 \ pi $.

In alcuni altri casi il numero di parametri disponibili nel problema non è sufficiente per rendere l'equazione adimensionale. In questi casi i fisici ricorrono a parametri fisici generici chiamati unità. Il loro unico scopo è rendere tutti i parametri nelle equazioni matematiche adimensionali (numeri puri).

I fisici spesso violano la regola che prescrive la matematica senza dimensioni. Quindi vedrai equazioni come

$$x^2+y^2=r^2$$

A rigor di termini questo non è corretto. Tuttavia, le persone tendono a interpretarlo come una scorciatoia per $$ (x / 1m) ^ 2 + (y / 1m) ^ 2 = (r / 1m) ^ 2 $$

(o con qualsiasi altra lunghezza unità di scelta al denominatore). Questo rende l'equazione di nuovo adimensionale. Direi che ciò che si intende veramente, tuttavia, è $$ (x / r) ^ 2 + (y / r) ^ 2 = 1 $$

Anche equazioni come

$$ \ ln x - \ ln r = 2 \ pi $$

in senso stretto non ha molto senso. Ancora una volta, le persone potrebbero trasformare questa assurdità in qualcosa di significativo interpretandola come una scorciatoia per

$$ \ ln (x / 1m) - \ ln (r / 1m) = 2 \ pi $$

Ciò che si intende veramente, tuttavia, è

$$ \ ln (x / r) = 2 \ pi $$

La conclusione è che non ha senso avere una lunghezza nuda $ x $ o una lunghezza nuda $ r $ nelle equazioni. Non ha nemmeno senso avere un solo milione di dollari. Tuttavia ha senso avere un parametro $ \ frac {r} {1 m} $ o $ \ frac {x} {r} $. È sempre così, ma diventa più evidente quando la funzione in questione assume, ad esempio, la forma di un logaritmo.