Un breve riassunto del documento citato in un'altra risposta e un altro buon sito.

Fondamentalmente gli aerei volano perché spingono abbastanza aria verso il basso e ricevono una spinta verso l'alto grazie alla terza legge di Newton.

Lo fanno in una varietà di modi, ma i contributi più significativi sono:

• L'angolo di attacco delle ali, che utilizza la resistenza per spingere l'aria verso il basso. Questo è tipico durante il decollo (si pensi agli aeroplani che salgono con il naso all'insù) e l'atterraggio (flap). Questo è anche il modo in cui gli aerei volano capovolti.
• La forma asimmetrica delle ali che dirige l'aria che passa sopra di loro verso il basso invece che direttamente dietro. Ciò consente agli aerei di volare a livello del suolo senza avere un angolo permanente sulle ali.

Le spiegazioni che mostrano un profilo alare senza un angolo di attacco non sono corrette. Le ali dell'aeroplano sono attaccate ad un angolo in modo da spingere l'aria verso il basso e la forma del profilo alare consente loro di farlo in modo efficiente e in una configurazione stabile .

Questa incidenza significa che anche quando l'aereo è a zero gradi, l'ala è ancora a un angolo di 5 o 10 gradi.

- Qual è il grado più comune per l'angolo di incidenza nei 747, 757 e 767?

Qualsiasi oggetto con un angolo di attacco in un fluido in movimento, come una piastra piana, un edificio o l'impalcato di un ponte, genererà una forza aerodinamica (chiamata portanza) perpendicolare al flusso. I profili alari sono forme di sollevamento più efficienti, in grado di generare più portanza (fino a un certo punto) e di generare portanza con meno resistenza.

- Profilo alare

Questa risposta non è altro che una variazione della risposta di Sklivv. Desidero semplicemente discutere alcune idee quantitative che derivano dalla risposta di Sklivv e discutere quello che ho capito (da un amico di ingegneria aerospaziale) come un errore concettuale comune - che l'applicazione di "semplici effetti di superficie" e "l'applicazione del principio di Bernoulli" è sbagliata. Questi "semplici effetti di superficie e il principio di Bernoulli" derivano dall'idea di Sklivv come spero di chiarire. Tutto nella fisica degli aeroplani inizia e finisce con "gli aeroplani spingono l'aria verso il basso, quindi l'aria spinge gli aeroplani in alto" . Questa risposta è scritta per essere comprensibile a qualcuno come me che non sa nulla di dinamica dei fluidi, a parte:

1. I problemi 2D matematicamente eleganti e completamente divertenti affrontati con la teoria delle variabili complesse (vedere Trovare punti di stagnazione dal potenziale complesso);

2. So che c'è in palio un premio Clay Mathematics per chiunque possa provare l'esistenza di, o fornire un controesempio contro l'esistenza di soluzioni fluide e ben definite a livello globale alle equazioni di Navier-Stokes;

3. Che colleghi e amici di ingegneria aerospaziale mi dicono che la prova sperimentale è ancora la regina in questo campo : la maggior parte della dinamica dei fluidi reali che coinvolge il volo in aereo si basa fortemente su modelli fenomenologici messi a punto dall'esperimento.

Risponderò riprendendo a turno questi punti.

L'esperimento è la regina

Da un particolare punto di vista sperimentale , non c'è mistero sul perché gli aeroplani volano. Piuttosto, la domanda migliore, a mio parere, è "come fanno a controllare le inevitabili enormi forze di portanza su di loro per fare in modo che queste ultime si sollevino stabilmente in una direzione verticale costante?"

Questa visione sperimentale è la seguente: pensa alla scala Beaufort e ad altre scale usate dai meteorologi per capire il significato pratico del loro vento e altri avvertimenti: ad esempio la scala Fujita per i tornado e i sistemi di categoria dei cicloni tropicali, che descrivono in termini pratici gli effetti di tempeste di varia intensità.

Ora capisco che i regolamenti di volo vietano agli aerei di linea commerciali di volare a una velocità inferiore a $ 300 \ mathrm {km \, h ^ {- 1}} $ prima del loro avvicinamento finale alla pista. Pensa a $ 300 \ mathrm {km \, h ^ {- 1}} $ velocità in termini di scale di cui ho appena parlato: questo è un tornado F4, ciclone di categoria 5 ed è ben al di fuori della scala Beaufort di 12 classi. Edifici e strutture di qualsiasi forma, delle dimensioni e del peso di aeroplani a pieno carico, vengono fatti a pezzi e portati in cielo o completamente abbattuti e distrutti. NON c'è carenza di portanza da una velocità relativa di $ 300 \ mathrm {km \, h ^ {- 1}} $ per sostenere quasi tutto ciò che ha le dimensioni e il peso di un aereo di linea commerciale a pieno carico: a queste velocità, quasi qualsiasi cosa di queste dimensioni e peso e mosche più leggere. Almeno lo fa fugacemente: se non è progettato come un aeroplano, mentre si muove il suo assetto cambia e così cambia la direzione della pressione dell'ariete: è quindi probabile che venga capovolto e precipitato catastroficamente a terra. In parole povere: quasi tutto vola a questa velocità, ma solo cose molto speciali lo fanno stabilmente.

Semplici modelli matematici

Possiamo fare un back of the stima dell'inviluppo della pressione del pistone in questo caso: vedere il disegno sotto di un semplice profilo alare con un angolo di attacco significativo tenuto fermo in una galleria del vento. Metterò alcuni numeri nella descrizione di Sklivvz:

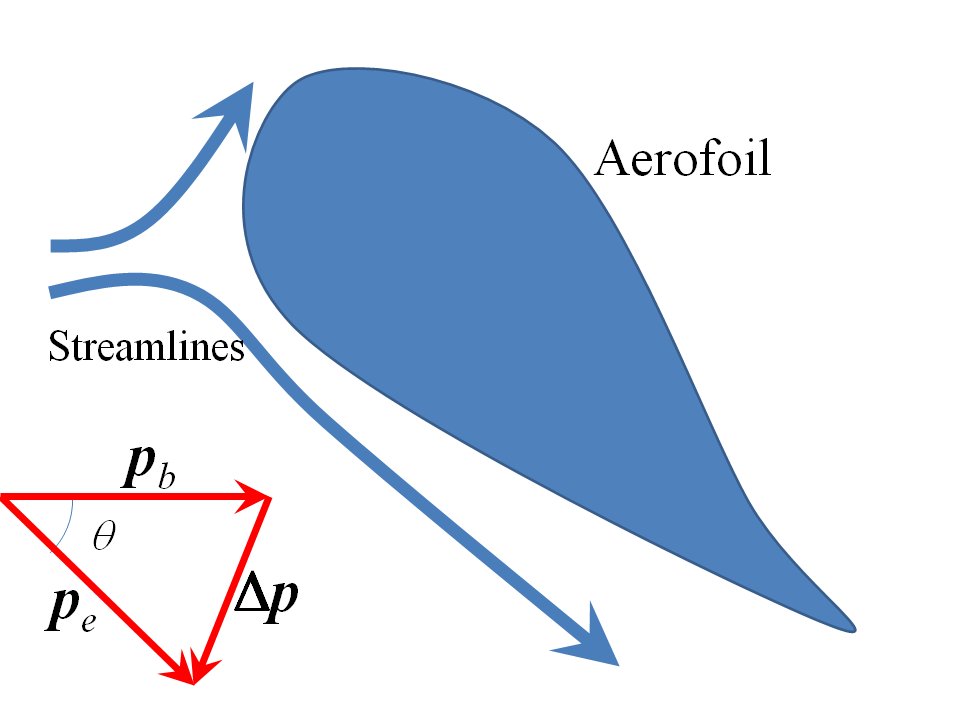
Supponiamo che il flusso d'aria venga deviato di un angolo $ \ theta $ radianti per modellare l'assetto di un aeroplano (non l'altitudine!) nel suo ultimo avvicinamento all'atterraggio o durante il decollo, volando a $ 300 \ mathrm {km \, h ^ {-1}} $ velocità relativa o circa $ 80 \ mathrm {m \, s ^ ​​{- 1}} $. L'ho disegnato con un angolo di attacco ripido. L'aria vicino alla pressione atmosferica a livello del mare ha una densità di circa $ 1,25 \ mathrm {kg \, m ^ {- 3}} $ (volume molare di $ 0,0224 \ mathrm {m ^ {- 3}}) $. Viene mostrato il diagramma della variazione della quantità di moto, da cui deriva la variazione delle componenti della quantità di moto verticale e orizzontale (assumendo che la velocità del flusso rimanga approssimativamente costante):

$$ \ Delta p_v = p_b \ sin \ theta; \ quad \ quad \ Delta p_h = p_b \, (1- \ cos \ theta) $$

Allo stesso tempo, l'ala deviante presenta un'efficace area di blocco al fluido di $ \ alpha \, A \ , \ sin \ theta $ dove $ A $ è l'area effettiva dell'ala e $ \ alpha $ un fattore di scala per tenere conto del fatto che nello stato stazionario non solo il fluido proprio accanto all'ala è distrubato in modo che l'area effettiva dell'ala lo essere più grande della sua area effettiva. Pertanto, la massa d'aria deviata ogni secondo è $ \ rho \, \ alpha \, A \, v \, \ sin \ theta $ e la portanza $ L $ e trascina $ D $ (che forza i motori devono permettersi al decollo ) deve essere:

$$ L = \ rho \, \ alpha \, A \, v ^ 2 \, (\ sin \ theta) ^ 2; \ quad \ quad D = \ rho \, \ alpha \, A \, v ^ 2 \, (1- \ cos \ theta) \, \ sin \ theta $$

Se inseriamo un angolo di attacco di 30 gradi, assumiamo $ \ alpha = 1 $ e usiamo $ A = 1000 \ mathrm {m ^ 3} $ (approssimativamente la cifra per un'area alare di un Airbus A380), otteniamo una forza di sollevamento $ L $ per $ \ rho = 1,25 \ mathrm {kg \, m ^ {- 3}} $ e $ v = 80 \ mathrm {m \, s ^ ​​{- 1}} $ di 200 tonnellate di peso. Questo è un po 'meno del peso al decollo di un Airbus A380 a pieno carico (che è di 592 tonnellate, secondo la pagina di Wikipedia A380) ma è un peso sorprendentemente alto lo stesso e nel giusto ordine di grandezza. Come ho detto, l'esperimento è la regina qui. Vediamo che la sezione trasversale verticale effettiva dell'ala è più grande dell'ala effettiva di un fattore da 2 a 3. Ciò non sorprende allo stato stazionario, ben al di sotto della velocità del flusso del suono: il fluido si accumula e il disturbo è molto più grande del semplice intorno al quartiere dell'ala. Quindi, inserendo un $ \ alpha = 3 $ (dato il fatto sperimentale che l'A380 può decollare a 592 tonnellate di peso lordo a pieno carico), otteniamo una resistenza di $ D $ di 54 tonnellate di peso (538kN) - circa la metà degli Airbus spinta completa di 1.2MN, quindi si collega bene con le specifiche effettive dell'Airbus, dato che deve esserci un comodo margine per sollevare l'aereo fuori difficoltà quando necessario.

In questi venti di grado F4 / C5 (e fino a tre volte più veloce in volo normale), vediamo quindi semplicemente che non c'è carenza di portanza. Il problema dell'ingegneria aeronautica riguarda più il mantenere questa portanza abbondante stabilmente diretta verso l'alto e consentire all'aereo di mantenere un assetto stabile e impedire a qualsiasi coppia derivante dalla non uniformità di portanza di ribaltare l'aereo.

Man mano che l'aereo prende velocità, la pressione del pistone calcolata sopra è proporzionale al quadrato della velocità relativa (vedi la mia risposta a Forza di trascinamento ad alta velocità), in modo che a piena velocità l'effetto più che spiega il calo della densità dell'aria e l'angolo di attacco più basso - non possiamo fare questa pressione del pistone verso il basso senza superare la componente posteriore orizzontale molto maggiore - la resistenza - quindi è importante volare con un angolo di attacco basso per una buona efficienza del carburante. / p>

Affinamento del modello matematico

È importante tenere presente che la descrizione di cui sopra in termini di differenza di momento tra l'aria in entrata e il flusso discendente generato dall'ala è esattamente la stessa fisica come le descrizioni "più popolari" fornite in termini di equazione di Bernoulli e integrazione della pressione attorno all'ala. Questo è facile da vedere: l'equazione di Navier-Stokes ( Vedi la pagina di Wikipedia per la derivazione dell'equazione di Navier-Stokes), è un'applicazione molto semplice di nient'altro che La seconda e la terza legge di Newton ai volumi infiniti di fluido, nonostante la mancanza di conoscenza delle sue proprietà matematiche fondamentali (come dichiarato dallo status non rivendicato del Clay Mathematics Millenium Prize: Adoro l'equazione di Navier-Stokes, un'idea così semplice e prontamente compresa così apertamente solo un'incarnazione delle leggi di Newton, ma che solleva misteri profondi che mostrano a noi scienziati quanto poco sappiamo ancora del mondo). L'equazione di Navier Stokes allo stato stazionario per un fluido perfetto e incomprimibile è (qui $ \ vec {v} $ è il campo di velocità allo stato stazionario e $ p $ il campo di pressione scalare):

$$ (\ vec {v} \ cdot \ nabla) \ vec {v} = \ nabla \ left (\ frac {| \ vec {v} | ^ 2} {2} \ right) + \ nabla \ wedge (\ nabla \ wedge \ vec {v}) = - \ nabla p $$

che restituisce $ \ nabla \ left (p + \ frac {| \ vec {v} | ^ 2} {2} \ right) = 0 $ o $ p + \ frac {| \ vec {v} | ^ 2} {2} = \ text {const} $ per un flusso irrotazionale ($ \ nabla \ wedge \ vec {v} = \ vec {0} $) quando integrato lungo la curva integrale di $ \ vec {v} $, cioè uno streamline. Oppure, in alternativa, possiamo argomentare in un modo più primo principio in questo semplice caso: la forza su un volume infinito è $ - \ nabla p $ e l'accelerazione di una particella sullo streamline è, mediante l'applicazione delle formule di Serret-Frenet (qui $ s $ è la lunghezza dell'arco lungo la linea di flusso attraverso la particella e $ \ kappa $ la curvatura del percorso):

$$ \ mathrm {d} _t (v \ hat {\ mathbf {t} }) = \ mathrm {d} _s v \ times \ mathrm {d} _t s \, \ hat {\ mathbf {t}} + v \, \ mathrm {d} _s (\ hat {\ mathbf {t}} ) \, \ mathrm {d} _t s = v \, \ mathrm {d} _s v, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} = \ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf { n}} $$

da cui, applicando $ \ vec {F} = m \ vec {a} \ Rightarrow - \ nabla p \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm {d} z = \ rho \, \ vec {a} \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm {d} z $, otteniamo:

$$ - \ nabla p = \ rho \ left (\ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} \ right) $$

che di nuovo restituisce $ p + \ frac {| \ vec {v} | ^ 2} {2} = const $ quando integrato lungo una linea di flusso (qui possiamo vedere la forza centripeta laterale (normale per razionalizzare) $ -v ^ 2 \, \ hat {\ mathbf {n}} / R $ dato dalla solita $ v ^ 2 / R $ formula). Quindi possiamo (e lo faremo, di seguito), ad esempio, applicare il Teorema di Blasius per calcolare la portanza, e essere certi che non è altro che una quantificazione dell'idea di Sklivv che "gli aeroplani spingono l'aria verso il basso, quindi l'aria spinge gli aeroplani in alto ". La differenza di pressione tra la superficie superiore e quella inferiore di un'ala esiste perché l'ala spinge l'aria verso il basso, non un fenomeno separato. Spesso si sente dire che il principio di Bernoulli applicato alle ali è sbagliato: questo non è vero. C'è un errore (da discutere più avanti) come mostrato dall'esperimento (e, ondeggiando con la mano, dalla teoria) nella solita dimostrazione della portanza usando il principio di Bernoulli, ma l'idea è fondamentalmente valida, come deve essere dalla sua derivazione dal Equazione di Navier-Stokes e leggi di Newton mostrate sopra.

Calcolo del profilo alare di Joukowsky ed errori nell'applicazione abituale del principio di Bernoulli alle ali

Esaminiamo un calcolo 2D della portanza in base al principio di Bernoulli o, equivalentemente, mediante l'applicazione del Teorema di Blasius. L'idea sbagliata comune qui è che i flussi d'aria si dividono al bordo d'attacco dell'ala e due particelle vicine raggiungeranno il bordo in ritardo dell'ala allo stesso tempo, in modo che le particelle superiori debbano affrontare la superficie curva a velocità più elevate e quindi la pressione sulla superficie dell'ala superiore è meno. In realtà, le particelle del percorso superiore sono accelerate molto più di quanto questa spiegazione implichi e raggiungono il bordo in ritardo dell'ala ben prima dei loro vicini del percorso inferiore. Guarda questo meraviglioso video dell ' Università di Cambridge, in particolare a circa 50 secondi dall'inizio. Questo fatto mostra che la circolazione $ \ oint_ \ Gamma \ vec {v} \ cdot \ mathrm {d} \ vec { r} $ attorno alla superficie dell'ala $ \ Gamma $ è diverso da zero, un fatto che ci aspettiamo intuitivamente da una semplice teoria (come mostrato sotto) e che è ampiamente confermato nell'esperimento: guarda il video, o vai alla fine di una pista di un grande aeroporto in una giornata umida in modo da poter far volare grandi aerei di linea commerciali a circa 50 m di altezza (prendere le cuffie). In una giornata umida, vedrai i vortici che si staccano dai bordi esterni delle ali, li vedrai turbinare nell'aria umida per molti secondi sulla scia dell'aereo e, se ti togli la protezione acustica dopo che l'aereo è passato, sentirai i vortici scoppiettano nell'aria, suonando un po 'come le onde che si bagnano sulla spiaggia. È molto più divertente di quanto sembri quando i tuoi figli ti chiedono di fare una cosa del genere e, dalle immagini e dai suoni, ho imparato molto di più dal farlo che pensavo di fare. Anche se il seguente calcolo ha un'aria di fondatezza teorica e di "primi principi", è importante capire che anch'esso è un modello sperimentale : la circolazione è forzata nella nostra descrizione, motivata dal conferma dell'esistenza del primo mediante esperimento. La condizione di Kutta-Joukowski (vedi la pagina di Wikipedia per la condizione di Kutta) così come la la pagina di Wikipedia per il teorema di Kutta-Joukowski sono poco più di una soluzione ad hoc motivata sperimentalmente : è semplicemente questo. Quando modelliamo il flusso con un profilo alare Joukowski (descritto di seguito), c'è un bordo affilato e in ritardo sull'ala. Ciò genera una singolarità con velocità infinite e non fisiche. Tuttavia, postulando e scegliendo la giusta circolazione nel flusso, possiamo mettere un punto di stagnazione sul bordo di ritardo, annullando così la singolarità, regolarizzando la nostra soluzione e anche forzando la condizione osservata sperimentalmente che c'è sempre un solo punto di stagnazione in corrispondenza dell'ala all'avanguardia, mai altrove.

Un altro modo per guardare a questa condizione motivata sperimentalmente è ben spiegato in questa risposta alla domanda di Physics SE un'ala in un flusso potenziale ha portanza?. Un flusso irrotazionale, invisibile, incomprimibile non può sollevare da solo un'ala. Aggiungiamo la circolazione a "fudge" una compensazione per questa mancanza teorica: la viscosità è "il modo in cui la natura impone la condizione di Kutta-Joukowsski".

Quindi iniziamo con il metodo delle variabili complesse (vedi Wikipedia pagina per "Flusso potenziale" nella sezione "Analisi per flusso bidimensionale" per studiare un flusso potenziale, ovvero campo di velocità irrotazionale ($ \ nabla \ wedge = \ vec {0} $) $ \ vec {v} $ con un potenziale $ \ psi $ tale che $ \ vec {v} = - \ nabla \ psi $ che è anche incomprimibile (equazione di continuità $ \ nabla \ cdot \ vec {v} = \ nabla ^ 2 \ psi = 0 $ ). Vedi anche le domande su Physics SE Trovare punti di stagnazione dal potenziale complesso).

Il metodo principale qui è usare la trasformata di Joukowski:

$ $ \ omega (z, \, s_z, \, s_ \ omega) = \ frac {s_ \ omega} {2} \ left (\ frac {z} {s_z} + \ frac {s_z} {z} \ right) $$

per mappare il flusso potenziale corrispondente a un cilindro rotante e sfalsato ( vedere la pagina della NASA "Sollevamento di un cilindro rotante") nel flusso intorno all'immagine di questo cilindro sotto la trasformata di Joukowsky. veramente strano Flettner Airplane in realtà utilizzava cilindri rotanti anziché ali per volare con successo. La trasformazione di Joukowsky mappa il cerchio $ | z | = s_z $ sull'asse reale tra i punti $ \ omega = \ pm s_ \ omega $ nel piano $ \ omega $; questa sezione dell'asse reale tra $ \ omega = \ pm s_ \ omega $ è quindi il ramo tagliato per la trasformata inversa di Joukowski. La trasformata di Joukowsky è una mappatura due a uno, e i rami della trasformata inversa di Joukowski mappano l'intera sfera $ \ omega $ -Riemann (se definiamo la proiezione stereografica in modo che $ | z | = s_ \ omega $ sia l'equatore di $ \ omega $ -Riemann sfera) separatamente all'interno e al di fuori del cerchio $ | z | = s_z $ nel piano $ z $ (che all'esterno e all'interno possono essere della sfera $ z $ -Riemann, se la proiezione stereografica è scelta in modo che il cerchio $ | z | = s_z $ è l'equatore della sfera $ z $ -Riemann). La superficie $ \ omega $ -Riemann è realizzata tagliando due copie della sfera di Riemann lungo il ramo tagliato e cucendo insieme i bordi, per ottenere una doppia copertura di genere zero per la sfera $ \ omega $ -Riemann. Per questo problema, definisco il ramo tagliato in modo leggermente diverso dalla sezione dell'asse reale tra $ \ pm s_ \ omega $, lo definisco come il percorso:

$$ \ operatorname {Im} (\ omega) = h \ cos \ left (\ frac {\ pi} {2} \ operatorname {Re} (\ omega) \ right) $$

tra i due punti di diramazione con un parametro di altezza regolabile $ h $, per ragioni che diventeranno chiare.

Il raggio $ r $ del raggio del cilindro rotante viene scelto in modo che la superficie del cilindro passi per il punto $ z = + s_z $, che è il immagine di uno dei punti di diramazione nel piano $ \ omega $. Ciò consente di ottenere il bordo affilato che diventa il bordo in ritardo del nostro profilo alare.

Il potenziale complesso per il cilindro rotante è:

$$ \ Omega (z) = v \, e ^ {- i \ alpha} \, \ left (z- \ delta \ right) + \ frac {r ^ 2 \, v \, e ^ {+ i \ alpha}} {z- \ delta} + i \, a \, \ log \ left (z - \ delta \ right) $$

dove $ \ alpha $ è l'angolo di attacco, $ \ delta = \ delta_r + i \, \ delta_i $ è l'offset e $ r $ è il raggio del cilindro immerso in un flusso uniforme che converge a $ v $ metri al secondo lungo l'asse reale positivo, da $ z \ a \ infty $. I termini logaritmo e dipolo mettono un punto di diramazione e un polo al centro del cilindro, quindi il flusso è perfettamente valido all'esterno e sul cilindro. $ a $ è la circolazione. Se lasciamo che $ \ phi $ stia per la coordinata angolare che etichetta il bordo del cilindro, ci sono due punti di ristagno sul cilindro con coordinate angolari $ \ phi_ \ pm $ dove $ \ mathrm {d} _z \ Omega (z ) = 0 $, ie quando:

$$ e ^ {i \, (\ phi_ \ pm - \ alpha)} = -i \ frac {a} {2 \, v \, r} \ pm \ sqrt {1- \ left (\ frac {a} {2 \, v \, r} \ right) ^ 2} = \ exp \ left (- \ arcsin \ frac {a } {2 \, v \, r} \ right) $$

Ora, mappiamo questo flusso al piano $ \ omega $ e applichiamo il Teorema di Blasio al immagine del cerchio di offset in modo da calcolare l'alzata su questa immagine. L'immagine può essere tracciata con il comando Mathematica:

$$ \ small {\ mathrm {P [\ delta_r \ _, \ delta_i \ _]: = \\ ParametricPlot [\ {Re [\ omega [ \ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]], Im [\ omega [\ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]] \}, \ {\ theta, 0, 2 \ pi \}]}} $$

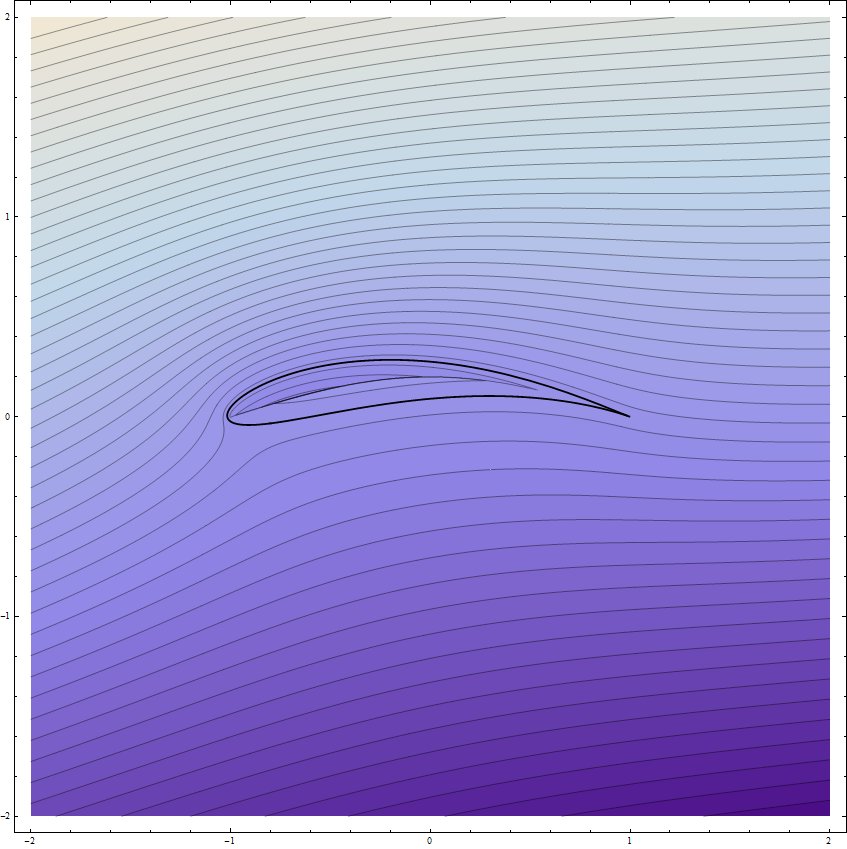
e il risultato viene disegnato sotto nel piano $ \ omega $ per $ s_z = s_ \ omega = 1 $, $ \ delta_r = -0.1 $, $ \ delta_i = 0.3 $ ( ie il cerchio rotante si sposta in modo che sia il centro è a $ -0.1 + i \, 0.2 $ e con un raggio $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $ in modo che la sua immagine passi per il punto di diramazione $ \ omega = + s_ \ omega = 1 $ nel piano $ \ omega $:

Ora veniamo al postulato cruciale di Kutta-Joukowski, un "fudge" sperimentale. Il bordo tagliente sul profilo al di sopra normalmente mapperebbe il flusso nel piano $ z $ in modo che ci fosse una velocità infinita non fisica in questo punto acuto. In pratica, nei test in galleria del vento si è visto che le linee di aerazione rimangono tangenti alla superficie superiore e che c'è un punto di ristagno sul bordo d'attacco dell'ala (intuitivamente l'aria "si schianta" qui) e nessun altro punti di ristagno sulla parte superiore o inferiore dell'ala. A volte c'è una piccola regione di turbolenza attorno al bordo in ritardo dell'ala (come nel video dell'Università di Cambridge) (cioè il modello di flusso potenziale incomprimibile qui fallisce) o il flusso si stacca dolcemente dal bordo in ritardo. Il modo in cui otteniamo effetti simili all'esperimento e "rinormalizzare" la nostra soluzione consiste nell'aggiungere la giusta quantità di circolazione $ a $ al flusso in modo che uno dei punti di ristagno sul cilindro rotante sia mappato sul bordo tagliente (il punto $ \ omega = + s_ \ omega $) nel piano $ \ omega $: la stagnazione annulla così le velocità infinite altrimenti non fisiche lì e "regolarizza" la nostra soluzione. Con il raggio del cilindro scelto come $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $, può essere facilmente mostrato dall'equazione sopra per le posizioni del punto di stagnazione che la circolazione necessaria è:

$$ a = 2 v \, \ delta_i \ cos \ alpha + 2 \, v \, (1- \ delta_r) \ sin \ alpha $$

Questa è quindi la condizione di Kutta-Joukowski interamente motivata sperimentalmente. È motivato dalla consapevolezza che la circolazione è osservata intorno alle ali, c'è sperimentalmente un solo punto di ristagno sul bordo d'attacco dell'ala e dal fatto che la giusta quantità di circolazione può riprodurre questi risultati visti sperimentalmente.

Quando questo è fatto, il calcolo della portanza del teorema di Blasius fatto attorno al profilo alare di Joukowski trasformato nel piano $ \ omega $ è:

$$ \ begin {array} {lcl} D_ \ ell - i \, L_ \ ell & = & \ frac {i \, \ rho} {2} \ oint _ {\ Gamma_ \ omega} (\ mathrm { d} _ \ omega \ Omega) ^ 2 \, \ mathrm {d} \ omega \\ & = & \ frac {i \, \ rho} {2} \ oint _ {\ Gamma_z} (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {d} z \\ & = & - \ pi \, \ rho \ Sigma [\, \ mathrm {residui \, di \,} \, (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {at \, poles \, entro \,} \ Gamma ] \\ & = & -4 \, \ pi \, i \, \ rho \, a \, v \, e ^ {- i \, \ alpha} \ end {array} $$

dove $ \ Gamma_ \ omega $ è il profilo alare di Joukowski e $ \ Gamma_z $ il profilo alare trasformato ( cioè il cilindro rotante). Quindi non c'è ascensore senza circolazione. Vale la pena ribadirlo:

Un flusso irrotazionale, invisibile, incomprimibile non può sollevare da solo un'ala. Aggiungiamo la circolazione a "fudge" una compensazione per questa mancanza teorica: la viscosità è "il modo in cui la natura impone la condizione di Kutta-Joukowsski".

Ora sostituiamo la condizione di Kutta-Joukowski per ottenere:

$$ D_ \ ell + i \, L_ \ ell = 8 \, \ pi \, i \, \ rho \, v ^ 2 \, \ left (\ delta_i \, \ cos \ alpha + (1- \ delta_r) \, \ sin \ alpha \ right) \ frac {s_z ^ 2} {s_ \ omega} e ^ {+ i \ alpha} $$

Ora dobbiamo ridimensionare le velocità in modo che le velocità relative siano uguali nei piani $ \ omega $ - e $ z $.

Quanto sopra è la forza per unità di lunghezza (in direzione normale alla pagina) sull'ala e la sua direzione è la direzione nel piano $ \ omega $. Abbiamo:

$$ \ lim \ limits _ {\ omega \ to \ infty} \ left (\ mathrm {d} _ \ omega \ Omega (\ omega (z)) \ right) = \ lim \ limits_ {z \ to \ infty} \ left (\ mathrm {d} _z \ Omega (\ omega (z)) \ right) \ lim \ limits _ {\ omega \ to \ infty} \ left (\ mathrm {d} _ \ omega z \ right) = 2 \, e ^ {- i \ alpha} v \ frac {s_z} {s_ \ omega} $$

quindi abbiamo bisogno di $ s_ \ omega = 2 $ e $ s_z = 1 $, quindi $ \ delta $ sarà un parametro adimensionale che definisce l'offset del cilindro $ z $ -piano come una frazione del suo raggio. Ma ora la larghezza del piano $ \ omega $ -piano dell'ala è di 4 unità. Inoltre, il calcolo precedente produce la forza per unità di lunghezza (normale al flusso 2D). Quindi dividiamo il risultato per $ s_ \ omega = 2 $ e $ s_z = 1 $ per 4 e poi aumentiamo la scala per l'area totale dell'ala per ottenere la forza totale sull'ala. Inoltre, dobbiamo ruotare il flusso nello schizzo qui sotto in modo che il flusso in entrata sia orizzontale (cioè nella direzione della velocità relativa dell'aria dell'aereo) nella $ \ omega $ -la forza totale sull'ala sopra diventa:

$$ D + i \, L = \ pi \, i \, \ rho \, v ^ 2 \, A \, \ left (\ delta_i \, \ cos \ alpha + (1- \ delta_r) \, \ sin \ alpha \ right) $$

Siamo testimoni del paradosso d'Alembert: il flusso perfetto non può modellare la resistenza. Ora inseriamo alcuni numeri. Se mettiamo $ \ delta = 0 $, allora l'ala è semplicemente il ramo diritto tagliato tra $ \ omega = \ pm 1 $, quindi abbiamo una versione del calcolo con cui ho iniziato ma ora perfezionato per tenere conto del modello di flusso completo. Con $ \ alpha = 0.3 $ (poco meno di 20 gradi), $ \ rho = 1.25 \ mathrm {kg \, m ^ {- 3}} $, $ v = 80 \ mathrm {m \, s ^ ​​{- 1}} $ e $ A = 850 \ mathrm {m ^ 2} $, otteniamo $ L = 643 \ mathrm {tonnellata} $, abbastanza vicino al peso al decollo a pieno carico dell'Airbus. Se abbiamo scelto i parametri $ \ delta_i = 0.2 $, $ \ delta_r = -0.1 $ per dare una forma dell'ala che non sembra troppo fantasiosa per un'ala di aereo di linea con i lembi del bordo in ritardo avvolti completamente per il decollo e l'atterraggio (vedere la trama sotto) otteniamo circa 1200 tonnellate di sollevamento per la nostra velocità di $ 300 \ mathrm {km \, h ^ {- 1}} $. Chiaramente questo è ottimistico e l'overreckonning deriva dal presupposto di uguale efficacia dell'intera apertura alare, mentre le punte chiaramente non saranno ben modellate dal flusso 2D. Non tutte le ali funzioneranno come modellate, quindi $ A $ in questa formula è un po ' inferiore rispetto all'area della forma della pianta. Ciò che il modello di flusso mostra (vedi sotto), tuttavia, è che l'effettiva sezione trasversale verticale presentata all'aria in ingresso è molto maggiore dell'area inclinata $ A \, \ sin \ theta $ assunta nel modello molto semplice all'inizio della mia risposta. Allo stato stazionario, una considerevole sezione trasversale dell'aria sia sopra che sotto la sezione trasversale verticale è piegata verso il basso e contribuisce all'effetto "gli aeroplani spingono l'aria verso il basso, quindi l'aria spinge gli aeroplani in alto" descritto nella risposta di Sklivv.

Ora, per tracciare il flusso trasformato completo nel piano $ \ omega $, dobbiamo usare la trasformata inversa di Joukowski. Per farlo con successo, è necessario utilizzare i rami giusti della trasformata inversa nelle patch di coordinate giuste. Per Mathematica, che pone il ramo tagliato per la funzione radice quadrata lungo l'asse reale negativo (lo spazio dei nomi std :: sqrt in Microsoft Visual C ++ lo colloca lungo l'asse reale positivo ), definiamo le seguenti funzioni del grafico, che sono rami particolari della trasformata inversa:

$$ \ zeta_1 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ left (\ omega + s_ \ omega \ right)} \ right) $$$$ \ zeta_2 (\ omega) = \ frac {s_z} { s_ \ omega} \ left (\ omega + i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ left (\ omega + s_ \ omega \ right)} \ right) $$$$ \ zeta_3 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$$$ \ zeta_4 (\ omega) = \ frac { s_z} {s_ \ omega} \ left (\ omega + \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$

e quindi i seguenti comandi di Mathematica tracceranno il flusso completo:

$$ \ small {\ mathrm {\ Omega [z \ _, \, \ delta \ _, \, v \ _, \, r \ _, \, a \ _, \, \ alpha \ _, \, s \ _]: = v \, e ^ {- i \, \ alpha} \ sinistra (\ frac {z} {s} - \ delta \ destra) + \ frac {r ^ 2 \ , v \, e ^ {i \, \ alpha}} {\ frac {z} {s} - \ delta} + i \, a \, Log \ left [\ frac {z} {s} - \ delta \ right]}} $$$$ \ small {\ mathrm {G [z \ _, \, \ delta_r \ _, \, \ delta_i \ _, \, \ alpha \ _]: = \ Omega \ sinistra [z, \, \ delta_r + i \, \ delta_i, \, 1, \, \ sqrt {(1- \ delta_r) ^ 2 + \ delta_i ^ 2}, 2 \, \ delta_i Cos [\ alpha] + 2 \, (1- \ delta_r) \, Sin [\ alpha], \, \ alpha, \, 1 \ right]}} $$

$$ \ small {\ mathrm {S [\ delta_r \ _, \ delta_i \ _, \ alpha \ _, h \ _, c \ _]: = \\ Mostra [ContourPlot [Im [If [(Abs [x] < 1) \ wedge (y > 0) \ wedge (y < h \, Cos [\ pi x / 2]), G [\ zeta_1 [x + iy], \ delta_r, \ delta_i, \ alpha]], Se [x < 0, G [\ zeta_3 [x + iy], \ delta_r, \ delta_i, \ alpha]], G [\ zeta_4 [x + iy], \ delta_r, \ delta_i, \ alpha ]]]]], \ {x, -2, 2 \}, \ {y, -2, 2 \}, Contours \ to c, MaxRecursion \ to 2, PlotPoints \ to 300, AspectRatio \ to 1], P [\ delta_r, \ delta_i, \ {Black, Thick \}]]}} $$

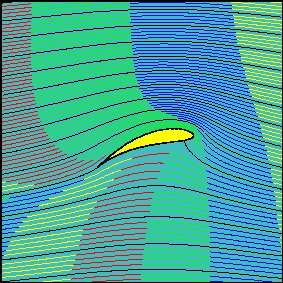
dove $ \ mathrm {P} [] $ è il comando di trama parametrico sopra usato per tracciare il profilo alare. L'uso precedente delle funzioni di ramo funziona per $ \ delta_r < 0 $: sono necessari altri rami per risultati corretti quando $ \ delta_r > 0 $. Il parametro $ h $ piega il ramo tagliato in modo che si pieghi verso l'alto e rimanga all'interno del profilo alare, consentendo così ai rami della trasformata inversa di Joukowsky di tracciare correttamente il flusso del cilindro mappato. Di seguito è disegnato il risultato del comando $ \ mathrm {S [-0.1, 0.2, 0.2, 0.2, 100]} $, ie il flusso attorno all'ala per un angolo di attacco di 0.2 radianti, i parametri di offset del cerchio di $ -0,1 + 0,2 \, i $, un arco nel ramo tagliato in modo che $ h = 0,2 $. Osserva il ramo tagliato all'interno del profilo alare sottostante e anche quanto lontano dalla superficie dell'ala si estende il suo effetto. La componente verticale effettiva dell'area dell'ala che viene presentata al flusso è chiaramente molto maggiore della componente verticale effettiva dell'area dell'ala, quindi il fattore di scala da 2 a 3 nell'ascensore dell'A380 come calcolato dal semplice calcolo della deflessione del fluido sembra altamente plausibile e non sorprende.

Infine, per chiudere il cerchio, ecco un'animazione che si trova nelle pagine web "Flussi sul piano irrotazionale di un fluido invisibile" a dipartimento di ingegneria ambientale dell'Università di Genova; vedi http://www.diam.unige.it/~irro/. L'animazione mostra l'andamento delle particelle fluide per il flusso del profilo alare di Joukowski, illustra l'affermazione che il flusso sopra l'ala attraversa l'ala molto più rapidamente del flusso sottostante e, infine, mostra molto bene la tesi principale che "gli aerei spingono l'aria verso il basso".

Da Stick and Rudder di Wolfgang Langewiesche, pagina 9, pubblicato nel 1944:

Il fatto principale di tutti i più pesanti il volo aereo è questo: l'ala mantiene l'aereo in alto spingendo l'aria verso il basso .

Spinge l'aria verso il basso con la sua superficie inferiore e tira l'aria verso il basso con la sua parte superiore superficie; quest'ultima azione è la più importante. Ma la cosa veramente importante da capire è che l'ala, in qualunque modo, fa scendere l'aria. Esercitando una forza verso il basso sull'aria, l'ala riceve una controforza verso l'alto - in base allo stesso principio, noto come legge di azione e reazione di Newton, che fa rinculare una pistola mentre spinge il proiettile in avanti; e ciò fa sì che l'ugello di una manichetta antincendio prema pesantemente all'indietro contro il vigile del fuoco mentre spara un flusso d'acqua in avanti. L'aria è pesante; l'aria a livello del mare pesa circa 2 libbre per iarda cubica; quindi, quando le tue ali spingono verso il basso a un metro cubo dopo un metro cubo di quella roba pesante, ottengono reazioni verso l'alto ugualmente pesanti.

Questo è ciò che tiene alto un aeroplano. La legge di Newton dice che, se l'ala spinge l'aria verso il basso, l'aria deve spingere l'ala verso l'alto. Mette la stessa cosa anche al contrario: se l'ala deve sostenere l'aereo nell'aria fluida e sempre cedevole, può farlo solo spingendo l'aria verso il basso. Tutta la fisica stravagante del Teorema di Bernoulli, tutta la matematica intellettuale della teoria della circolazione, tutti i diagrammi che mostrano il flusso d'aria su un'ala - tutto questo è solo un'elaborazione e una descrizione più dettagliata di come la legge di Newton si adempia - per esempio, l'osservazione piuttosto interessante ma (per il pilota) davvero del tutto inutile che l'ala fa la maggior parte del suo lavoro di downwash per aspirazione, con la sua superficie superiore. ...

Quindi, se dimentichi un po 'di questa eccessiva erudizione, un'ala diventa molto più facile da capire; in ultima analisi non è altro che un deflettore d'aria. È un piano inclinato, abilmente curvo, certo, ed elaboratamente aerodinamico, ma ancora essenzialmente un piano inclinato. Dopo tutto, questo è il motivo per cui tutto il nostro affascinante aggeggio è chiamato aeroplano.

Dato che hai chiesto una spiegazione appropriata a un pubblico non specializzato, forse questo andrà bene: " A Physical Description of Flight; Revisited" di David Anderson & Scott Eberhardt. È una revisione della precedente " Descrizione fisica del volo" ( versione HTML).

Senza entrare nei meccanismi eccellenti e dettagliati che spiegano l'aumento della reazione che altri hanno fornito per questa risposta, voglio solo dire che contrariamente alla credenza popolare / ai libri di testo di fisica delle scuole superiori, gli aeroplani non volano esclusivamente per il principio di Bernoulli. Secondo l'eccellente "For the Love of Physics" di Walter Lewin:

"Il principio di Bernoulli rappresenta il 20% della portanza di un aeroplano, il resto è fornita dalla portanza di reazione."

Walter Lewin pone anche una domanda perspicace se gli aerei volano davvero a causa della teoria del transito uguale e del principio di Bernoulli (non lo fanno!).

"... allora come fanno gli aerei a volare sottosopra?"

Le ali forniscono portanza perché dirigono l'aria verso il basso.

Dirigono l'aria verso il basso in due modi. In parte, la parte inferiore dell'ala si inclina leggermente verso il basso e spinge semplicemente l'aria verso il basso mentre si muove in avanti nell'aria. Ma questo è un piccolo effetto. La parte superiore dell'ala è più importante.

La parte superiore dell'ala abbassa parzialmente l'aria fornendo una rampa. La parte posteriore della parte superiore dell'ala è inclinata verso un bordo di uscita affilato. L'aria, che è sotto pressione dalle miglia d'aria sopra di essa, segue quella pendenza lungo l'ala e continua verso il basso dopo che l'ala è passata.

Ma c'è molto di più. Mentre l'ala si spinge in avanti, l'aria che viene deviata verso l'alto dal bordo d'attacco finisce per essere schiacciata tra gli strati d'aria sopra e la parte superiore sporgente dell'ala. Quel pizzicamento fa accelerare l'aria, non diversamente dal modo in cui pizzicare un seme di anguria bagnato può farlo volare. L'inerzia dell'aria che è più lontana dall'ala costringe l'aria che è più vicina all'ala ad abbracciare la superficie superiore dell'ala, raggiungendo il bordo d'uscita molto prima delle molecole corrispondenti che si sono dirette lungo la parte inferiore.

L'asimmetria, ovviamente, è la chiave qui. La parte inferiore dell'ala è più quasi parallela al percorso dell'aria, con una leggera pendenza verso il basso fino alla parte posteriore, quindi non ha lo stesso effetto di pizzicamento. (L'asimmetria non deve essere nella forma dell'ala. Può essere tutto nell'angolo di attacco. Stai ancora creando uno scenario in cui l'aria è più pizzicata da una parte che dall'altra.)

Ovviamente non esiste un confine netto tra gli strati d'aria che stanno pizzicando e l'aria che viene pizzicata. Tuttavia, la forza dell'ala è percepita in modo più forte dall'aria più vicina, e quindi quello strato è più accelerato. Ogni pezzetto d'aria pizzica l'aria sotto e viene schiacciato contro l'aria sopra, in misura decrescente, finché l'effetto non è più percepibile a una certa distanza sopra l'ala.

Tutta quest'aria accelerata è soggetta all'effetto Bernoulli. Poiché è stato accelerato, la sua pressione verso il basso sull'ala è inferiore alla pressione verso l'alto dell'aria sottostante, e anche la pressione verso l'alto sull'aria sopra è inferiore alla pressione ambiente. Ciò fa sì che ancora più aria si muova verso il basso di quanto non lo farebbe altrimenti. A meno che non sbagli, questa è una parte importante della deviazione dell'aria verso il basso.

Il mito, quindi, non è che l'effetto Bernoulli sia importante. Il mito è che esista un principio di parità di tempo che è la ragione per cui l'aria in cima all'ala si muove più velocemente.

Ma la spiegazione è ancora incompleta perché il principio di Bernoulli stesso non è ovvio. Il principio è spesso spiegato in termini di bassa pressione che causa l'accelerazione: se crei un'area di bassa pressione, l'aria accelererà effettivamente verso di essa. Ma se soffi in un tubo con una costruzione, la diminuzione della pressione alla costrizione cercherà di restringerla di più. La pressione a monte dai polmoni sta davvero causando la diminuzione della pressione; non è solo la pressione più bassa a far fluire l'aria.

Il modo in cui una maggiore pressione nei polmoni può causare una diminuzione della pressione alla costrizione è che i polmoni danno slancio all'aria. Quando l'aria finalmente lascia il tubo, lo slancio viene assorbito dall'aria circostante, spingendola indietro come una folla che si spinge in una folla in piedi. Questo slancio impedisce che parte della contropressione venga avvertita dall'aria in movimento nel tubo. Maggiore è la velocità, minore è la densità di momento e minore è la contropressione.

In effetti, in un modello stazionario, invisibile e incomprimibile, la domanda su cosa causa ciò che diventa quasi privo di significato. L'aria accelera perché c'è una pressione più bassa davanti e c'è una pressione più bassa davanti a causa della velocità dell'aria. Ma nel caso di un aereo, la mia comprensione è che la spinta dei motori sta causando l'accelerazione dell'aria più che semplicemente lasciando che la parte superiore inclinata verso il basso dell'ala si allontani da essa. Anche ad alte velocità subsoniche in cui l'aria non può più essere trattata come incomprimibile, si applica ancora il fenomeno qualitativo che una maggiore velocità porta a una pressione ridotta. Calcolare l'effetto diventa solo più complicato.

Spesso, il principio di Bernoulli è derivato usando la conservazione dell'energia lungo linee di flusso. Penso che la mia spiegazione qualitativa usando lo slancio sia coerente con questo.

Il principio della portanza viene spesso spiegato usando la circolazione. Di nuovo, penso che sia solo un modo diverso di descrivere lo stesso processo. Le diverse velocità lungo la parte superiore e quella inferiore costituiscono una circolazione netta.

Nota: vedere " Perché l'aria scorre più velocemente sopra la parte superiore di un profilo alare?" per ulteriori risposte a quella parte della questione dell'ascensore.

Sono in ritardo per la festa qui e penso che i migliori votanti (Sklivvz, niboz) abbiano risposto adeguatamente, ma darò comunque i miei due centesimi:

Ci sono diversi modi per spiegare come vola un aeroplano. Alcuni sono più dettagliati di altri e, sfortunatamente, le spiegazioni più popolari sono sbagliate. Ecco alcune spiegazioni utili, a seconda del pubblico:

• La spiegazione più semplice è che l'ala spinge l'aria verso il basso e secondo la terza legge di Newton l'aria esercita una forza uguale ma opposta verso l'alto . Il modo principale in cui ciò avviene è tramite l'angolo di attacco, ma anche la forma dell'ala gioca un ruolo importante. Questo è sufficiente per la maggior parte delle persone e dovrebbe essere la spiegazione predefinita.

• Una spiegazione più dettagliata tratterebbe della differenza di pressione tra i due lati dell'ala, poiché la portanza è una forza meccanica, deve essere esercitato sulla superficie dell'ala e l'unico modo in cui l'aria può farlo è attraverso la pressione. Quindi deve esserci una regione di bassa pressione sulla parte superiore dell'ala e maggiore pressione sulla parte inferiore. Da dove viene questo? Proviene dall'aria che cambia direzione mentre scorre intorno all'ala. Ogni volta che l'aria cambia direzione e segue un percorso che è curvo, ci sono gradienti di pressione con una pressione inferiore all'interno della curva.

• Una spiegazione ancora più dettagliata sarebbe esaminare le equazioni di Navier-Stakes e tutta la matematica che ne consegue. Questo va oltre lo scopo di questa risposta.

Holger Babinsky ha scritto un documento molto leggibile chiamato "How Do Wings Work?" che consiglierei. Copre abbastanza bene la risposta centrale (e confuta molte delle spiegazioni senza senso che purtroppo sono fin troppo comuni). Conoscere un po 'di calcolo è utile, ma penso che l'articolo sia leggibile senza di esso. Vedi http://iopscience.iop.org/0031-9120/38/6/001/pdf/pe3_6_001.pdf

La risposta di Nib è corretta. La risposta altamente votata da Sklivvz inizia promettente ma poi inserisce alcune affermazioni errate:

Le spiegazioni che mostrano un profilo alare senza un angolo di attacco non sono corrette. Le ali dell'aeroplano sono attaccate ad un angolo in modo da spingere l'aria verso il basso e la forma del profilo alare consente loro di farlo in modo efficiente e in una configurazione stabile.

Questa incidenza significa che anche quando l'aereo è a zero gradi, l'ala è ancora a un angolo di 5 o 10 gradi.

Un profilo alare asimmetrico crea portanza a AoA zero. Tutti i velivoli ad ala fissa hanno profili alari asimmetrici, solo gli elicotteri usano profili alari simmetrici nel rotore (a causa di questi non hanno momento torcente). Gli aeromobili ad ala fissa hanno una torsione alare: hanno un angolo di attacco positivo alla radice, un AoA negativo in punta e un AoA medio il più vicino possibile allo zero, per ridurre al minimo la resistenza.

In effetti ciò che fa volare l'aereo è deviare una corrente d'aria verso il basso. Un piatto piano può farlo, e Bernoulli non ha posto in un piatto piano. I velivoli subsonici non usano piastre piatte perché creano una grande quantità di resistenza ad angoli di attacco diversi da zero - infatti in un flusso turbolento, anche una piastra piatta a AoA zero crea più resistenza di un profilo alare simmetrico come NACA 0012 .

Considera il campo di velocità delle particelle nella massa d'aria in una proiezione 2D degli assi X (avanti) e Z (su). Per ogni particella, integrare su area e tempo, per ricavare il centro della quantità di moto della massa d'aria (p) prima e dopo il passaggio dell'aereo: dp / dt. (In una mattina molto calma, senza vento o turbolenza, il centro della massa d'aria e la sua quantità di moto sono stazionari in Z (presumete il volo livellato non accelerato), e uguale alla vera velocità relativa in X che punta nella direzione poppa -X . Integra sull'area e scoprirai che il centro e la quantità di moto della particella e il campo del vettore sono cambiati, con il passaggio del piano. Questo centro della massa d'aria e il centro della quantità di moto si sposteranno in avanti (+ X) e verso il basso (-Z ) rispetto al suo stato originale. La variazione della quantità di moto uguale e opposta con il tempo dp / dt dell'aereo è una forza. Potremmo etichettare la componente -X "trascinamento" e la componente + Z "portanza" (attenzione: il sistema di coordinate dell'aeroplano è diverso dalla massa d'aria stazionaria). Questo è un sistema dissipativo, quindi non aspettare troppo a lungo dopo il passaggio dell'aereo per registrare il campo vettoriale. Possiamo osservare questo processo in scie di condensazione nelle giornate limpide quando l'aria di alta quota è fredda e relativamente Sfortunatamente, poiché li vediamo principalmente dal basso con una proiezione lungo il Z, ci manca la componente discendente del campo momentum. Puoi vederlo come un pilota collaudatore, che vola come inseguitore alare, in formazione (proiezione nel piano Y-Z da dietro o X-Z dal lato). Espandi questo modello in 3D per includere il flusso e gli effetti dell'asse laterale o Y! Suggerisco che questo "p-punto" (dp / dt) della spiegazione del cambio di quantità di moto sia migliore, piuttosto che "spingere" o "tirare" l'aria verso il basso, perché il secondo può confondere la posizione e lo slancio nella vista del lettore. Questo è anche il primo termine (LHS) nella bellissima equazione di Eulero-LaGrange, che porterebbe a un'analisi ancora più elegante di questa domanda!

Come nuovo utente, dovrò capire come allegare le figure e le equazioni appropriate a questo post ...- grazie

Nota: l'equazione della resistenza è in realtà la legge dei gas ideali, tranne per il fatto che la densità sostituisce m / V.

P / rho = R T:

Essenzialmente un aereo ad ala fissa vola perché si muove nell'aria e ha un'ala fissa che è angolata nella direzione del flusso d'aria. Una componente della forza di resistenza che agisce sull'ala agisce nella direzione (su) opposta alla direzione (giù) della forza del peso dell'aereo.

L'ala di un aereo si comporta come una banderuola che risponde al flusso d'aria relativo. L'effetto di base può essere ottenuto con una piastra rigida e piatta e una fonte di movimento in avanti come un'elica, gravità o momento di lancio (ad esempio aerei di carta per bambini). Sono stati introdotti perfezionamenti (come le sezioni trasversali del profilo alare) per mitigare gli effetti collaterali indesiderati delle piastre piatte (come lo stallo).

Nessun grande argomento con le altre risposte popolari qui, ma cercherò di spiegare il nozioni di base sulle ali fisse in termini di collisioni molecolari . Quella che segue è una spiegazione piuttosto semplificata (ignorando cose come temperatura, densità, viscosità, compressibilità, taglio, strati limite, turbolenza, vortici, resistenza di forma, rugosità alare, rigidità, attrito della pelle, stallo, trasmissione per reazioni a catena, coppie di forze ecc. ).

Un esperimento mentale. Ti siedi in fondo a una piscina profonda e piena d'acqua. In una mano tieni una mazza da ping pong. Allunga il braccio e cerca di spazzare la mazza orizzontalmente a velocità costante attraverso l'acqua con la faccia della mazza prima (a) verticale, poi (b) orizzontale, quindi (c) da qualche parte nel mezzo.

Nel caso (a) la faccia del pipistrello è verticale e ci sarà la massima resistenza al movimento in avanti. La resistenza al movimento in avanti può essere spiegata da due ampi effetti.

Il primo effetto è perché le molecole d'acqua che si scontrano con e rimbalzano elasticamente dalla faccia anteriore della mazza lo fanno leggermente più velocemente e più frequentemente (in media) rispetto alle molecole d'acqua che colpiscono la faccia posteriore il pipistrello. Questa è una semplice conseguenza del movimento della mazza in avanti e della conservazione della quantità di moto lineare negli urti elastici (si pensi alle palle da biliardo che colpiscono uno specchio d'acciaio grande, massiccio, rigido, liscio e piatto). Ogni collisione provoca un cambiamento nella velocità della mazza. Poiché le collisioni frontali sono in media più veloci e più frequenti delle collisioni posteriori, l'effetto netto sarà quello di ridurre la velocità di avanzamento della mazza. Per mantenere la mazza in movimento a velocità costante attraverso l'acqua, dovrai spendere energia muscolare per lavorare contro la resistenza.

Il secondo effetto segue dal primo effetto. Le molecole che entrano in collisione con la parte anteriore della mazza verranno spostate in avanti provocando un aumento della pressione (un effetto ariete). Questo aumento di pressione agirà per aumentare ulteriormente le velocità delle molecole d'aria e i tassi di collisione sulla faccia anteriore della mazza. La zona di maggiore pressione crescerà di dimensioni prima del pipistrello. Nel tempo la continua crescita della zona di alta pressione sarà compensata dalla diffusione laterale dell'energia cinetica (molecole ad alta velocità che donano parte della loro velocità alle molecole circostanti che si muovono più lentamente da collisioni elastiche) e dal flusso di massa delle molecole oltre i bordi del pipistrello alle aree a pressione più bassa sul retro della mazza.

Nel caso (b) la faccia della mazza è orizzontale e la mazza scivola nell'acqua con relativamente poca resistenza.

Nel caso (c) la faccia del pipistrello è inclinata. L'entità della resistenza dipende dall'angolo della faccia del pipistrello rispetto alla direzione del movimento. La resistenza è maggiore quando la faccia del pipistrello è quasi verticale (angolo di attacco ripido) rispetto a quando la faccia del pipistrello è quasi orizzontale (angolo di attacco basso). L'entità della resistenza dipende dall'apparente area della sezione trasversale della mazza rivolta nella direzione del movimento. A un angolo di attacco minore, un minor numero di molecole impattano la faccia del pipistrello, l'angolo medio di incidenza delle particelle che arrivano alla faccia del pipistrello è maggiore, causando un ridotto scambio di quantità di moto e c'è meno pressione a monte perché è più facile (meno ostruzione) per le molecole sfuggire al zona di alta pressione scorrendo oltre la mazza.

Quando la faccia della mazza è inclinata verso l'alto la forza netta sulla mazza è diretta non all'indietro orizzontalmente come nei casi (a) e (b) ma perpendicolarmente alla faccia del pipistrello (parte all'indietro e parte verso l'alto). Ciò può essere spiegato dalla geometria delle collisioni molecolari su una superficie piana che si muove attraverso un fluido stazionario.

Un aerodinamico classico potrebbe descrivere le accelerazioni perpendicolari alla faccia come la combinazione di componenti sia di resistenza (all'indietro) che di portanza (verso l'alto). Se inclini la mazza in modo che il bordo d'attacco sia inclinato verso il basso, la direzione netta della resistenza al movimento della mazza sarà in parte all'indietro (trascinamento) e in parte verso il basso ("sollevamento negativo"). L'uso incondizionato del termine "ascensore" può creare confusione. Potrebbe essere meglio fare riferimento a componenti della resistenza indotta dall'ala che operano in direzioni specifiche (ad esempio verso l'alto, perpendicolare al flusso d'aria principale, perpendicolare alla superficie alare, perpendicolare al piano orizzontale dell'aeromobile).

Puoi avere una buona sensazione per l'effetto di trascinamento indotto dalle ali tenendo la mano, piatta con le dita unite, fuori dal finestrino di un'automobile quando viaggia a velocità (diciamo 50 mph) e inclinando il palmo verso l'alto e e annotare le forze che senti quando cerchi di mantenere la tua mano nella stessa posizione. (Probabilmente è meglio non provare una racchetta da ping pong su strade pubbliche!).

Le interazioni dei fluidi con i corpi solidi dipendono dalle proprietà del fluido e dalla geometria dell'oggetto. Nel caso di un aeroplano, abbiamo l'aria come fluido e una geometria del profilo alare. La geometria del profilo alare è progettata appositamente per forzare il fluido al di sotto di esso preferenzialmente al di sopra di esso. Ciò si traduce in una differenza di pressione, che quindi porta a una forza di galleggiamento che accelera l'ala secondo la seconda legge di Newton (portanza). La legge di Bernoulli è rilevante per il calcolo del problema del fluido.

Quindi, per ottenere il volo, tutto ciò di cui hai bisogno sono alcuni profili alari ben progettati e un modo per impartire una velocità iniziale. Per continuare a volare devi mantenere alta la velocità e per continuare a volare in modo stabile hai bisogno di un aereo ben progettato con il centro di massa, il centro di spinta e il centro di portanza nella stessa posizione.

A causa dell'ostruzione dell'ala, l'aria deve girare intorno all'ala, quindi la pressione dell'aria nella parte inferiore dell'ala è aumentata perché l'aria nella parte inferiore dell'ala viene compressa per girare intorno all'ala, e l'aria nella parte superiore dell'ala è tesa attorno all'ala, quindi la pressione dell'aria nella parte superiore dell'ala diminuisce. Quindi c'è una differenza di pressione e poi c'è un sollevamento. Nota: la parte inferiore dell'ala è sopravento, quindi l'aria è compressa, la pressione è alta e la parte superiore dell'ala è sottovento, quindi l'aria è tesa e la pressione è bassa. Quindi la portanza non può essere spiegata dal teorema di Bernoulli. Perché il teorema di Bernoulli non considera la compressione e lo stretching del fluido.

La seguente è una spiegazione dettagliata:

Ad esempio, nella parte superiore dell'ala, la direzione della velocità dell'aria nel punto A è la direzione della freccia blu. Poiché la freccia blu è inclinata (notare l'angolo tra la freccia blu e la normale blu nell'immagine), la freccia blu tende ad essere lontana dall'ala lungo la direzione normale nella parte superiore dell'ala, quindi la pressione dell'aria a la parte superiore dell'ala è allungata, quindi la pressione dell'aria nella parte superiore dell'ala diminuisce, quindi c'è una differenza di pressione (gradiente di pressione). Questa differenza di pressione cambia la direzione della velocità dell'aria, quindi la direzione della velocità dell'aria nel punto B è la direzione della freccia rossa e anche la freccia rossa è inclinata ... Quindi la direzione della velocità dell'aria continuerà a cambiare lungo il parte superiore dell'ala. Va notato che questa differenza di pressione non solo cambia la direzione della velocità dell'aria sulla parte superiore dell'ala, ma genera anche la portanza dell'ala.

Se non c'è bassa pressione (pressione negativa) nella parte superiore dell'ala, il flusso d'aria si sposterà verso il basso?Ovviamente non si muoverà verso il basso.Il sollevamento dell'ala deriva dalla bassa pressione nella parte superiore dell'ala e dall'alta pressione nella parte inferiore dell'ala.Il movimento verso il basso del flusso d'aria è solo il risultato di alta e bassa pressione.Perché la parte superiore dell'ala è a bassa pressione?Perché il flusso d'aria tende a partire lungo la normale direzione dell'ala.Perché il fondo dell'ala è alto?Perché il flusso d'aria tende ad avvicinarsi lungo la normale direzione dell'ala.

L'interrogante continua a sollevare obiezioni a causa di altre forme di fuga che fa notare. Se definiamo il volo solo come un corpo che crea portanza usando un qualche modo per muovere aria pulita su un profilo alare, allora tutte le discussioni sul profilo alare sono totalmente corrette ei suoi esempi non sono rilevanti. Se allentiamo la nostra definizione di volo come il sollevamento di un corpo da terra per un periodo di sostegno oltre l'effetto di qualsiasi propulsione a terra iniziale, abbiamo ancora palloncini, razzi e, al punto, molti aerei leggeri con una spinta -peso rapporto> 1, consentendo loro di far volare l'aereo in stallo. L'Harrier e l'F-22 sono ottimi esempi e l'Osprey può essere lanciato per una discussione sul motivo per cui gli elicotteri volano.

In verità, tutto il volo più pesante dell'aria è una combinazione di almeno queste due semplici dinamiche di portanza del profilo alare e surplus di energia di spinta (quella riserva disponibile dopo aver soddisfatto il movimento in avanti per la portanza). E, naturalmente, l'intero calcolo relativo ai gradienti di portanza alare cambia oltre la velocità del suono e quindi a velocità ipersoniche.

È importante ricordare che per il volo a profilo alare è necessaria una velocità in avanti. Ciò significa che, senza una qualche forma di spinta interna, il volo del profilo alare più pesante dell'aria è solo una caduta prolungata nell'aria. Con qualsiasi fonte interna di propulsione per sostenere il volo, diamo anche al pilota un modo per creare un surplus di energia per manovrare, aumentare la velocità o guadagnare quota. Chiedere a un pilota come vola: "Angolo di attacco, velocità dell'aria, altitudine (ripetizione)". Il profilo alare è solo un componente.