Non c'è rigonfiamento delle maree.
Questo è stato uno dei pochi errori di Newton. Newton ha ottenuto la funzione di forzatura della marea corretta, ma la risposta a quella forzatura negli oceani: completamente sbagliata.
La teoria dell'equilibrio delle maree di Newton con i suoi due rigonfiamenti di marea è falsata dall'osservazione. Se questa ipotesi fosse corretta, l'alta marea si verificherebbe quando la Luna è allo zenit e al nadir. La maggior parte dei luoghi degli oceani terrestri ha un'alta marea ogni 12.421 ore, ma se queste alte maree si verificano allo zenit e al nadir è pura fortuna. Nella maggior parte dei luoghi, c'è uno scostamento prevedibile dallo zenit / nadir della Luna e dall'ora dell'alta marea, e tale scostamento non è zero.
Uno dei luoghi più confusi per quanto riguarda le maree è il cortile di Newton . Se la teoria dell'equilibrio di Newton fosse corretta, l'alta marea si verificherebbe più o meno nello stesso momento attraverso il Mare del Nord. Non è quello che si osserva. In qualsiasi momento della giornata, si può sempre trovare un luogo nel Mare del Nord con l'alta marea e un altro con la bassa marea contemporaneamente.
Perché non c'è un rigonfiamento?
Al di là delle prove, ci sono una serie di ragioni per cui non può esistere un rigonfiamento di marea negli oceani.
Il rigonfiamento di marea non può esistere a causa del modo in cui le onde dell'acqua si propagano. Se il rigonfiamento della marea esistesse, formerebbe un'onda con una lunghezza d'onda pari alla metà della circonferenza terrestre. Quella lunghezza d'onda è molto maggiore della profondità dell'oceano, il che significa che l'onda sarebbe un'onda poco profonda. La velocità di un'onda poco profonda in un punto è di circa $ \ sqrt {gd} $, dove $ d $ è la profondità dell'oceano in quel punto. Questo maremoto poteva muoversi solo a 330 m / s anche nella fossa oceanica più profonda, a 205 m / s sulla profondità media di 4267 m, e meno di quella in acque poco profonde. Confronta con la velocità di rotazione di 465 m / s all'equatore. L'onda di marea superficiale non può tenere il passo con la rotazione della Terra.
Il rigonfiamento della marea non può esistere perché la Terra non è completamente coperta dall'acqua. Ci sono due enormi barriere nord-sud al rigonfiamento della marea di Newton, le Americhe nell'emisfero occidentale e l'Afro-Eurasia nell'emisfero orientale. Le maree sulla costa del Pacifico di Panama sono molto, molto diverse dalle maree a soli 100 chilometri di distanza sulla costa caraibica di Panama.
Una terza ragione per cui il rigonfiamento della marea non può esistere è l'effetto Coriolis. Il fatto che la Terra stia ruotando a una velocità diversa da quella orbitale della Luna significa che l'effetto di Coriolis agirebbe per separare l'onda di marea anche se la Terra fosse completamente coperta da un oceano molto profondo.
Qual è il modello giusto?
Quello che Newton ha sbagliato, Laplace ha ragione.
La teoria dinamica di Laplace delle maree spiega i problemi menzionati sopra. Spiega perché è sempre alta marea da qualche parte nel Mare del Nord (e Patagonia, e la costa della Nuova Zelanda, e pochi altri luoghi sulla Terra dove le maree sono completamente pessime). Le funzioni di forzatura delle maree combinate con le profondità e i contorni del bacino oceanico danno luogo a sistemi anfidromici. Ci sono punti in superficie, "punti anfidromici", che non subiscono maree, almeno rispetto ad una delle tante funzioni di forzatura delle maree. Le risposte di marea ruotano attorno a questi punti anfidromici.
Esiste un gran numero di risposte in frequenza alle funzioni generali di forzatura della marea. La Luna è la forza dominante per quanto riguarda le maree. Aiuta a guardare le cose dalla prospettiva del dominio della frequenza. Da questa prospettiva, la frequenza dominante nella maggior parte dei luoghi della Terra è 1 ciclo ogni 12,421 ore, la frequenza di marea M 2 . Il secondo più grande è il ciclo 1 ogni 12 ore dovuto al Sole, la frequenza di marea S 2 . Poiché la funzione di forzatura non è del tutto simmetrica, ci sono anche 1 ciclo per 24.841 ore di risposte (la frequenza di marea M 1 ), 1 ciclo per 24 ore di risposte (la S 1 frequenza di marea) e una sfilza di altri. Ognuno di questi ha il proprio sistema anfidromico.
Per quanto riguarda il Mare del Nord, ci sono tre punti anfidromici di marea M 2 nelle vicinanze del Mare del Nord. Questo spiega bene perché le maree sono così sciocche nel Mare del Nord.
Immagini
Per coloro a cui piacciono le immagini, ecco alcune immagini chiave. Spero che i proprietari di queste immagini non riorganizzino i loro siti web.
La forza delle maree
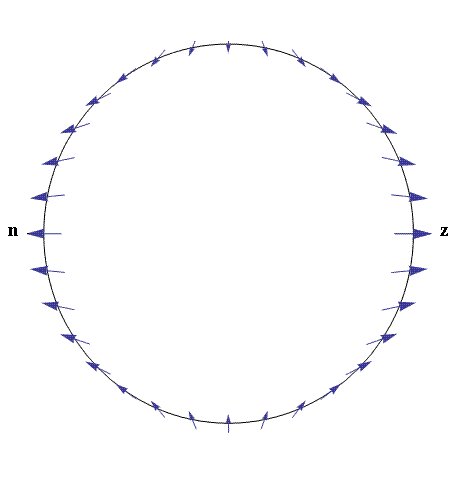
Fonte: https: // fisica .mercer.edu / hpage / tidal% 20asymmetry / asymmetry.html
Questo è ciò che Newton ha fatto bene. La forza di marea è lontana dal centro della Terra quando la Luna (o il Sole) è allo zenit o al nadir, verso l'interno quando la Luna (o il Sole) è all'orizzonte. La componente verticale è la forza trainante dietro la risposta della Terra nel suo insieme a queste forze di marea. Questa domanda non riguarda le maree della Terra. La domanda riguarda le maree oceaniche, ed ecco la componente orizzontale che è la forza trainante.
La risposta globale alle maree M 2
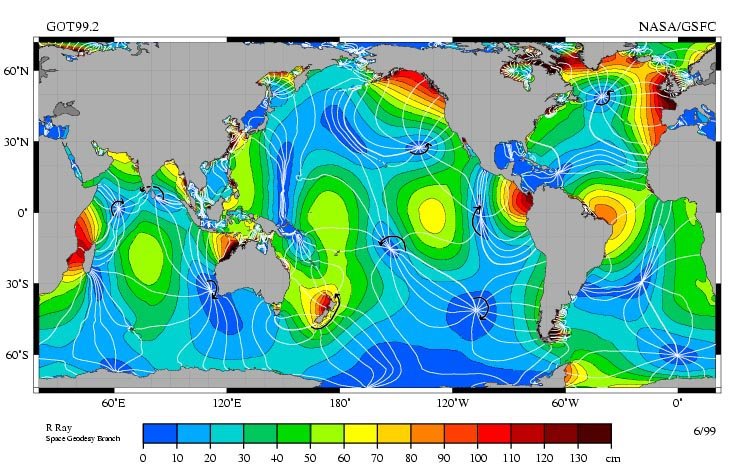
Fonte: https://en.wikipedia.org/wiki/File:M2_tidal_constituent.jpg
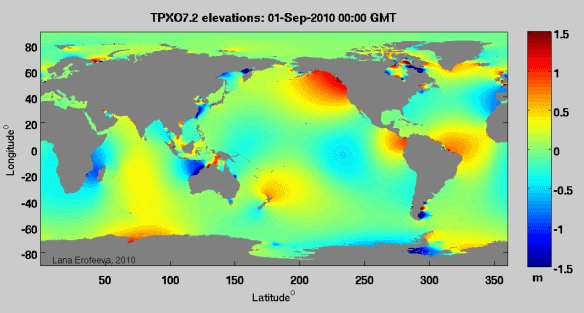
Fonte: http://volkov.oce.orst.edu/tides/global.html img
Il costituente M2 delle maree è la risposta all'incirca due volte al giorno alla funzione di forzatura della marea che risulta dalla Luna. Questa è la componente dominante delle maree in molte parti del mondo. La prima immagine mostra i punti anfidromici M2, punti in cui non è presente la componente M2 delle maree. Anche se questi punti hanno una risposta nulla a questo componente, questi punti anfidromici sono comunque critici nel modellare la risposta alle maree. La seconda immagine, una gif animata, mostra la risposta nel tempo.
La risposta alle maree M2 nel Mare del Nord
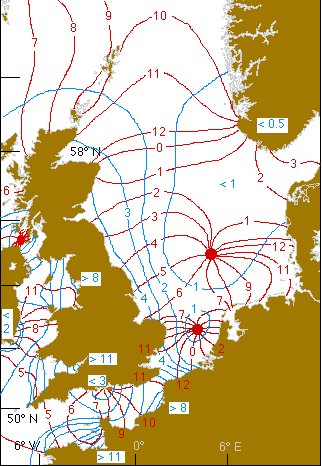
Fonte: https: / /www.geog.ucsb.edu/~dylan/ocean.html
Ho menzionato più volte il Mare del Nord nella mia risposta. Il Nord Atlantico è il luogo in cui si verifica il 40% della dissipazione della marea M2 e il Mare del Nord è il fulcro di questa dissipazione.
Flusso di energia del maremoto lunare semi-diurno (M2)
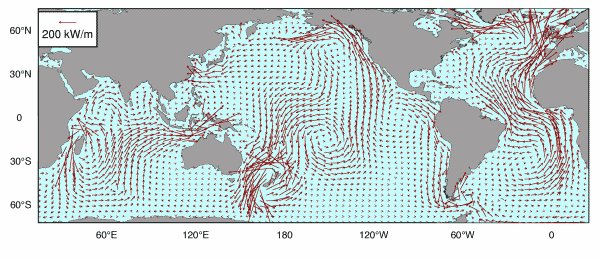
Fonte: http://www.altimetry.info/thematic-use-cases/ocean-applications/tides/ http://www.altimetry.info/ wp-content / uploads / 2015/06 / flux_energie.gif
L'immagine sopra mostra il trasferimento di energia dai luoghi in cui viene creata l'energia delle maree ai luoghi in cui viene dissipata. Questo trasferimento di energia spiega le strane maree in Patagonia, uno dei luoghi sulla Terra dove le maree sono più alte e più controintuitive. Quelle maree della Patagonia sono in gran parte il risultato del trasferimento di energia dal Pacifico all'Atlantico. Mostra anche l'enorme trasferimento di energia verso l'Atlantico settentrionale, dove si verifica il 40% della dissipazione delle maree M2.
Nota che questo trasferimento di energia è generalmente verso est. Puoi pensare a questo come a un "rigonfiamento netto della marea" che rappresenta. O no. Preferisco "o no".
Discussioni estese basate sui commenti (eliminiamo i commenti qui)
Uno tsunami non è un'onda di acque poco profonde rispetto ai bacini oceanici? So che la lunghezza d'onda è più piccola ma è ancora un'onda di acque poco profonde e quindi si propagherebbe alla stessa velocità. Perché non soffrono di ciò che hai menzionato riguardo alla velocità di rotazione della terra.
In primo luogo, c'è una grande differenza tra uno tsunami e le maree. Uno tsunami è il risultato di un oscillatore armonico smorzato non lineare (gli oceani terrestri) a un impulso (un terremoto). Le maree sono la risposta a una forza motrice ciclica. Detto questo,
- Come nel caso di qualsiasi oscillatore armonico, la risposta all'impulso è informativa della risposta a una forza motrice ciclica.
- Gli tsunami sono soggetti all'effetto Coriolis . L'effetto è piccolo, ma presente. Il motivo per cui è piccolo è perché gli tsunami sono, per la maggior parte, eventi a breve termine relativi alla velocità di rotazione della Terra. L'effetto di Coriolis diventa evidente nella risposta a lungo termine degli oceani a uno tsunami. La topografia è molto più importante per uno tsunami.
Il collegamento che segue fornisce un animazione dello tsunami del terremoto indonesiano del 2004.
Riferimenti per quanto sopra:
Dao, MH, & Tkalich, P. (2007). Modellazione della propagazione dello tsunami? uno studio di sensibilità. Rischi naturali e scienza del sistema terrestre , 7 (6), 741-754.
Eze, CL, Uko, DE, Gobo, AE, Sigalo, FB, & Israel-Cookey , C. (2009). Modellazione matematica della propagazione dello tsunami. Journal of Applied Sciences and Environmental Management , 13 (3).
Kowalik, Z., Knight, W., Logan, T., & Whitmore, P. (2005) . Modello numerico dello tsunami globale: tsunami indonesiano del 26 dicembre 2004. Science of Tsunami Hazards , 23 (1), 40-56.
Questa è una risposta interessante piena di fatti e diagrammi interessanti, ma penso che sia un po 'sopravvalutata. La spiegazione di Newton non era sbagliata, era un'approssimazione. Sapeva che era un'approssimazione: ovviamente era consapevole che la terra aveva terra oltre che acqua, che le maree avevano altezze diverse in luoghi diversi e così via. Non penso sia una coincidenza che l'altezza del rigonfiamento nell'equipotenziale sia quasi della dimensione giusta per spiegare le altezze osservate delle maree.
L'analisi di Newton è stata un buon inizio . Newton ha certamente descritto correttamente la forza delle maree. Non aveva gli strumenti matematici per fare meglio di quello che aveva. L'analisi di Fourier, il trattamento appropriato dei frame non inerziali e la dinamica dei fluidi sono tutti successivi alla data di Newton di circa un secolo.
Oltre alle questioni sopra citate, Newton ha ignorato la componente orizzontale della forza di marea e ha guardato solo la componente verticale. La componente orizzontale non sarebbe importante se la Terra fosse agganciata alla Luna in modo mareale. La teoria dinamica delle maree ignora essenzialmente la componente verticale e guarda solo la componente orizzontale. Questo fornisce un'immagine molto diversa delle maree.
Non sono l'unico a dire che il rigonfiamento della marea non esiste. Ad esempio, da questa lezione, la pagina sulle maree dinamiche chiede retoricamente "Ma come può l'acqua confinata in un bacino impegnarsi in un moto ondoso come i" rigonfiamenti di marea "che presumibilmente spazzare il globo come illustrato nella teoria dell'equilibrio? " e risponde immediatamente (enfasi mia) " La risposta è - non può. "
In Affholder, M., & Valiron, F. (2001). Oceanografia fisica descrittiva. CRC Press , gli autori introducono la marea di equilibrio di Newton ma poi scrivono (enfasi mia) "Affinché l'onda di marea si muova a questa enorme velocità di 1600 km / h, la profondità dell'oceano ideale avrebbe essere 22 km. Prendendo la profondità media dell'oceano come 3,9 km, la velocità delle elevazioni di marea può essere solo di 700 km / h. Pertanto la posizione di equilibrio in qualsiasi istante richiesta da questa teoria non può essere stabilita. "
Gli oceanografi insegnano ancora la teoria della marea all'equilibrio di Newton per una serie di ragioni. Fornisce un'immagine corretta della funzione di forzatura della marea. Inoltre, molti studenti non capiscono quanti posti possono avere due maree al giorno. Del resto, la maggior parte degli istruttori di oceanografia e degli autori di libri di testo non capiscono! Molti oceanografi e i loro testi sostengono ancora che il rigonfiamento interno è una conseguenza della gravità, ma l'altro rigonfiamento è una conseguenza di una cosiddetta forza centrifuga. Questo fa impazzire geofisici e geodocisti. Sta iniziando a cambiare; negli ultimi dieci anni circa, alcuni testi di oceanografia hanno finalmente iniziato a insegnare che l'unica forza necessaria per spiegare le maree è la gravitazione.