L'intera domanda è una premessa errata. Esistono sono galassie sferiche (o almeno quasi sferiche)! Si dividono in due categorie fondamentali: quelle galassie ellittiche di forma pseudo-sferica e le cosiddette "galassie sferoidali nane" molto più piccole che si trovano associate alla nostra galassia e ad altre grandi galassie in il "Gruppo locale".

Ovviamente quando guardi una galassia nel cielo è solo una proiezione bidimensionale della distribuzione reale, ma si può ancora dedurre la sfericità (approssimativa) dalla distribuzione della luminosità superficiale e dalla grande velocità della linea di vista distribuzione per molte ellittiche e sferoidali nane.

Le galassie sferoidali nane possono effettivamente essere il tipo più comune di galassia nell'universo.

Queste galassie sono approssimativamente sferiche perché le stelle si muovono in orbite con orientamenti abbastanza casuali, molti su orbite quasi radiali (altamente eccentriche) senza assi fortemente preferiti. La dispersione della velocità è solitamente molto più grande di qualsiasi segno di rotazione.

C'è un'ottima risposta a una domanda correlata a Perché le galassie formano piani 2D (o simili a spirale) invece di sfere 3D (o tipo sferico)?

Belle immagini: immagine di Schmidt nel Regno Unito della galassia sferoidale nana dello Scultore (credit: David Malin, AAO)

La galassia ellittica E0 M89 (credito Sloan Digitized Sky Survey).

Dettagli: ho trovato un paio di articoli che rafforzano l'argomento secondo cui molte galassie ellittiche sono quasi sferiche. Questi documenti sono di Rodriquez & Padilla (2013) e Weijmans et al. (2014). Entrambi questi articoli esaminano la distribuzione delle apparenti ellitticità delle galassie rispettivamente nel "Galaxy Zoo" e nello Sloan Digitized Sky Surveys. Quindi, con un modello statistico e con varie ipotesi (incluso che le galassie siano orientate casualmente), invertono questa distribuzione per ottenere la distribuzione della vera ellitticità $ \ epsilon = 1- B / A $ e un parametro oblato / prolato $ \ gamma = C / A $, dove i tre assi dell'ellissoide sono $ A \ geq B \ geq C $. cioè È impossibile dire se una galassia individuale dall'aspetto circolare vista in proiezione è sferica, ma puoi dire qualcosa sulla distribuzione delle forme 3D se hai un campione di grandi dimensioni.

Rodriguez & Padilla conclude che il valore medio di $ \ epsilon $ è 0,12 con una dispersione di circa 0,1 (vedi immagine sotto), mentre $ \ gamma $ ha una media di 0,58 con una dispersione più ampia (gaussiana) di 0,16, coprendo l'intera va da zero a 1. Dato che $ C / A $ deve essere inferiore a $ B / A $ per definizione, questo significa che molte ellittiche devono essere molto vicine a sferiche (non puoi dire che nulla è esattamente sferico ), sebbene la galassia "ellittica media" ovviamente non lo sia.

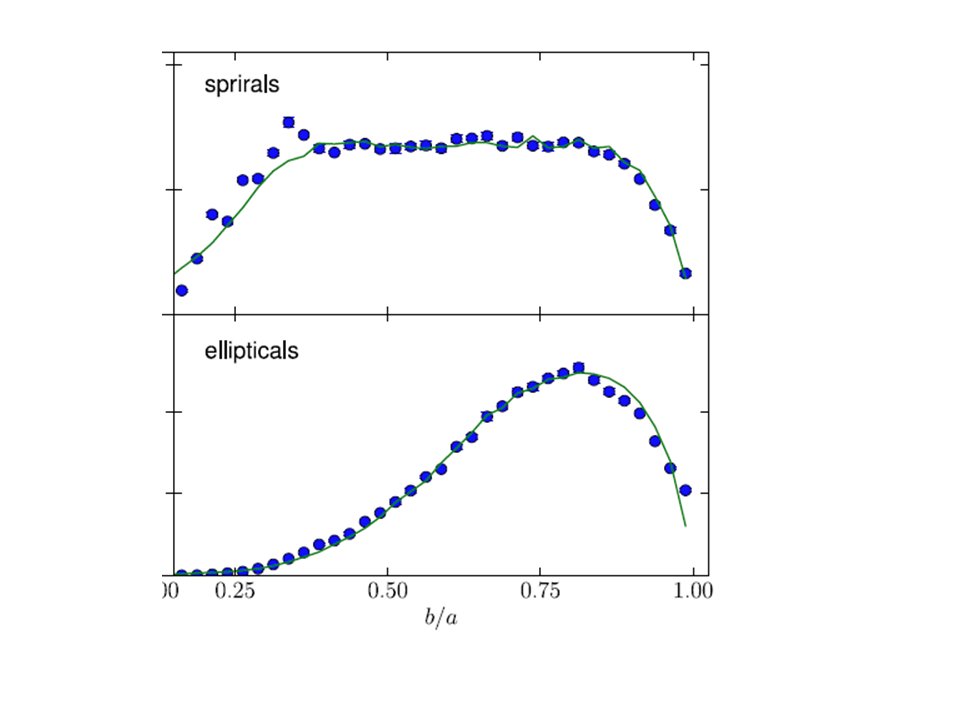
Questa immagine mostra la distribuzione osservata delle ellitticità 2D per un grande campione di galassie a spirale ed ellittiche. Le linee sono ciò che prevedi di osservare dalle distribuzioni di forma 3D trovate nel documento.

Questa immagine di Rodriguez e Padilla mostra le distribuzioni reali dedotte di $ \ epsilon $ e $ \ gamma $. La linea rossa continua rappresenta le ellittiche. Le medie delle distribuzioni sono indicate con linee verticali. Nota come la linea tratteggiata per le spirali ha un valore $ \ gamma $ molto più piccolo, perché sono appiattite.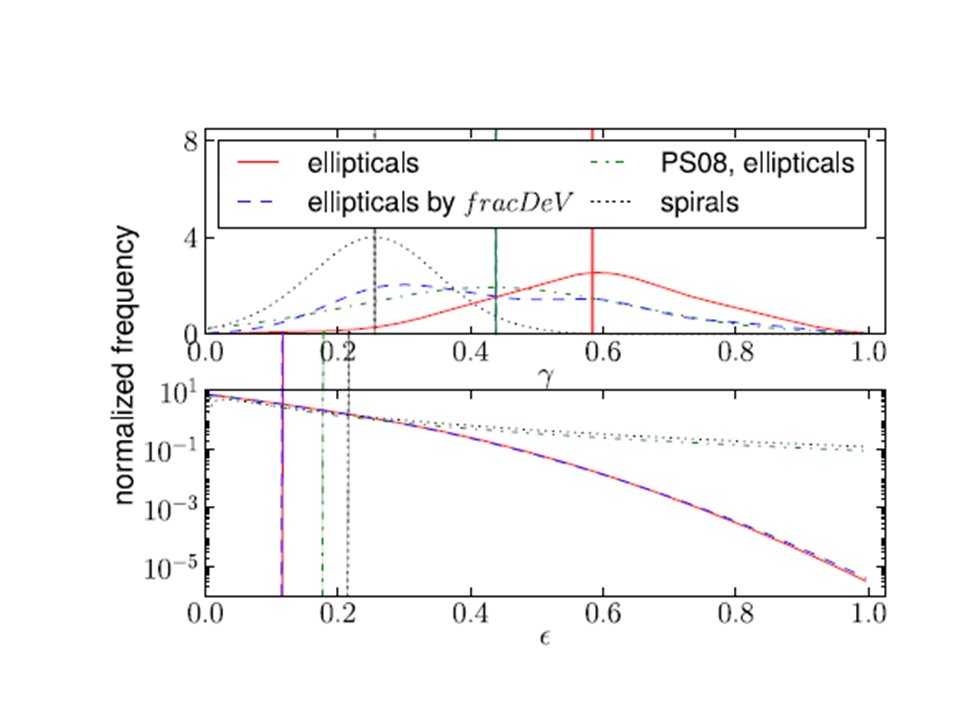

Weijmans et al. (2014) eseguono analisi simili, ma dividono il loro campione ellittico in quelli che hanno prove di una rotazione sistematica significativa e quelli che non lo fanno. Come ci si potrebbe aspettare, quelli rotanti sembrano più appiattiti e "oblati". Quelle a rotazione lenta possono anche essere modellate come galassie oblate, sebbene abbiano maggiori probabilità di essere "triassiali". I rotatori lenti hanno una media $ \ epsilon $ di circa 0,15 e una media $ \ gamma $ di circa 0,6 (in buon accordo con Rodriguez & Padilla), ma i campioni sono molto più piccoli.

In realtà, ci sono parti di una galassia che si estendono oltre il piano galattico:

• alone galattico: questo è in realtà la parte primaria di una galassia che non si trova nel disco galattico principale. È costituito da più sezioni ed è composto da una serie di oggetti.

  • Alone di materia oscura: questo è un sezione della materia oscura della galassia che esiste in una forma semisferica. Possiamo capire la dimensione e la forma dell'alone (sebbene sia tipicamente sferico) attraverso i suoi effetti sul movimento delle stelle su larga scala.

  • Galattico sferoide: questa è una regione vicino al centro della galassia composta da stelle con orbite dispari. Le considero una sorta di comete nella fascia di Kuiper, che seguono strane orbite 3D. Le stelle potrebbero essere state perturbate dal buco nero centrale nella galassia, nel nostro caso Sagittario A *.

  • Corona galattica: Bit di gas e polvere che seguono percorsi irregolari attraverso la galassia. Interagiscono con la materia all'interno del disco galattico e quindi oscillano.

• Rigonfiamento galattico: Questo è la parte centrale della galassia, attorno al buco nero supermassiccio centrale. Sono composti da gas, stelle e polvere.
• Flusso stellare: una serie di stelle che hanno interagito gravitazionalmente con un altro oggetto. Potrebbero essere i resti di una galassia nana.

Li elenco come esempi per mostrare che non tutti gli oggetti rimangono nel piano galattico. Le altre risposte dovrebbero darti un'idea del motivo per cui la maggior parte degli oggetti rimane sull'aereo.

Tutta la materia nella galassia deve ruotare (non necessariamente nella stessa direzione) in modo che agisca una forza centrifuga. Senza la forza centrifuga, tutta la materia contenuta nella galassia collasserà al centro della galassia a causa della gravitazione. La rotazione avviene attorno ad un asse, una linea attorno alla quale tutta la materia ruota nella galassia. Ora, il modo in cui tutta la materia ruota attorno a quell'asse è planare. Perché è planare e perché deve ruotare solo attorno a un asse? La risposta a questa domanda chiarirà definitivamente quel dubbio.

Ma come fa la galassia planare a mantenere la planarità per miliardi di anni?

Immaginiamo che una galassia planare ha pochi corpi che non ruotano attorno all'asse centrale e hanno un proprio asse di rotazione. In qualsiasi direzione perpendicolare a quell'asse, la forza centrifuga impedisce al corpo di collassare al centro della galassia. In qualsiasi direzione parallela a quell'asse, tuttavia, non vi è tale forza centrifuga; ma c'è una componente della forza gravitazionale della materia contenuta nella galassia planare sottostante. Questa componente della forza gravitazionale continua a tirare il corpo verso l'aereo e non c'è forza per fermarlo. Quindi, anche questo corpo finirà per unirsi al piano galattico. Tutti questi corpi marginali che non obbediscono al piano galattico saranno attratti dalla gravità per unirsi infine al piano. Pertanto la galassia riesce a mantenere la planarità.

Come ha sottolineato Rob Jeffries, ci sono galassie di forma sferica e altre forme tridimensionali. Lì, tuttavia, poiché non esiste un piano di rotazione preesistente , nulla fa collassare la materia in un piano. Pertanto, quelle galassie mantengono la loro forma tridimensionale.

È dovuto all'effetto combinato di rotazione e "dissipazione". Una nuvola di gas rotante è composta da particelle che interagiscono fortemente tra loro (collidendo fisicamente) su scale temporali relativamente brevi possono irradiare parte della loro energia e quantità di moto emettendo fotoni. Per entrambi questi motivi, una densa nube di gas rotante collasserà per formare un disco rotante. Ma ci sono alcuni sistemi stellari che rimangono piuttosto sferici, chiamati ammassi globulari.

D'altra parte, se il gas in una nuvola forma stelle molto rapidamente, in modo che le particelle in essa contenute siano stelle piuttosto che atomi, quindi queste "particelle" stellari non interagiscono fortemente su brevi scale temporali (per esempio il tempo tra le collisioni dirette per una stella in un ammasso globulare è> $ 10 ^ {10} $ anni, e gli ammassi globulari sono praticamente sferici) non possono irradiano la loro energia e quantità di moto emettendo fotoni; possono emettere radiazioni gravitazionali, ma non è altrettanto efficace

Per questi motivi, un ammasso sferico di stelle rimarrà sferico per periodi di tempo molto lunghi; molto più a lungo dell'attuale età dell'universo.

Hai menzionato galassie ellittiche, che le altre risposte non hanno toccato.

Contrariamente alla tua affermazione sulle galassie in 2D, le galassie ellittiche sono "tridimensionali" in la sensazione che le stelle non siano confinate su un piano; Potresti pensare che siano "a forma di uovo".

Allora perché le galassie ellittiche non sono confinate su un piano? Soprattutto perché (di solito) hanno un momento angolare basso, cioè non ruotano troppo velocemente su nessun asse, quindi il ragionamento nella risposta di Simha non si applica più.

Inoltre, vale la pena notare che questo non significa che non ci sia nessun movimento rotatorio. Non è necessario che la galassia nel suo insieme ruoti attorno a un asse, ma lo saranno le stelle all'interno della galassia. Le stelle si muoveranno tutte in modo abbastanza casuale all'interno della galassia ellittica, quindi il momento angolare netto è vicino allo zero.

A differenza di una galassia a spirale, la galassia nel suo insieme ha un momento angolare molto definito, quindi oltre alla velocità propria delle stelle (spesso chiamata velocità peculiare ), la stella ruoterà attorno al centro galattico nella stessa direzione delle sue vicine, e in effetti ogni altra stella della galassia.